RSA Algorithm In Asymmetric Key Cryptography – All You Want To Know !! [Includes Example As Well]
As we all know that there are two types of Cryptography present in the field of security i.e. Symmetric and Asymmetric key cryptography. So AES and DES Symmetric cryptography methods we have already seen in the previous posts.
Now in this post, we will explore the RSA algorithm in detail which is basically the foundation stone for the RSA Asymmetric cryptography process. Further, we will also look into an example of the RSA algorithm application to make the topic simpler .
First, we should recap the basics discussed earlier, there are total of three types of the key present in the cryptography method . These are mainly secret key , public key and private key . Out of these secret keys is used for the Symmetric cryptography process, whereas the other two i.e. public and private keys are used for the Asymmetric cryptography.
Public key algorithms also called asymmetric key algorithms. Two different keys are used during the encryption and decryption process (one key for encryption and second key used at the time of decryption). RSA algorithm is the best example of asymmetric key cryptography. The private key (only known to the owner) & Public key (possibly known to everyone) in the Asymmetric cryptography .
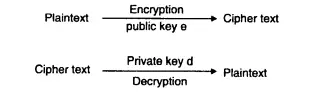
What Is The RSA Algorithm In Asymmetric Key Cryptography ?
The most common public key algorithm is RSA . Ron Rivest, Adi Shamir and Len Aldeman have developed this algorithm (RivestShamir-Aldeman) in 1978.
It is a public-key encryption algorithm. It is a block-cipher that converts plain text into cipher text at the sender side and vice versa at the receiver side. The algorithm works as follows :
Note : In the below steps the symbol ‘^’ represents raised to values for e.g. if 2^2 given that means 2 raised to the power 2 which is 4
1. Select two prime numbers a and b where a is not equal to b.
2. Calculate n = a * b
3. Calculate Φ(n) = (a-1) * (b- 1).
4. Select e such that, e is relatively prime to Φ(n) i.e. gcd (e, Φ(n)) = 1 and 1 < e < Φ(n).
5. Calculate of such that d = e^(-1) mod Φ(n) or ed mod Φ(n) = 1.
6. Public key = {e,n}, private key = {d,n).
7. Find out ciphertext using the formula.
C = P^e mod n where, P < n and
C = Ciphertext, P = Plaintext, e = Encryption key and n = Block size.
8. P = C^d mod n
Plaintext P can be obtain using the given above formula (step 8). Where, d = decryption key.
Both sender and receiver know the value of n. In addition, the sender must know encryption key ‘e’ and receiver must know decryption key ‘d’.
RSA Algorithm Example In Reality !!
Now its time for its application so that you can understand this concept in a well-applied manner indeed .
Let us now Calculate cipher text using RSA algorithm given data as follows: Prime numbers p, q as 7, 17 respectively and plain text message is to be sent is 10.
By using RSA algorithm as mentioned above [Refer the RSA algorithm above]
Step 1 : Prime numbers are 7 and 17 i.e. a = 7, b=17
Step 2 : value of n = a*b = 7 * 17 = 119.
Step 3 : Φ(n) = (a-1) * (b-1) = (7-1) * (17-1) = 6* 16 = 96
Step 4 : Select e such that it is relatively prime to Φ(n) i.e. gcd(e, Φ(n)) = 1
If we select e as 3 then it is not relatively prime p 96 because
e =1*3 and 96 =2*2*2*2*2*3 (gcd must be 1)
Hence , we select e as 5 (gcd must be 1)
Thus , e = 1*5
gcd (5, 96) = 1
Hence e = 5 (encryption key)
Step 5 : Now we have to calculate d such that
d = e^(-1) mod Φ(n)
Hence , e * d mod Φ(n) = 1 ,
i.e. 5 * d mod 96 = 1
Now using RSA algorithm we can compute the following :
d = ((Φ(n) * i) + 1 )/5 where i = 1 to 9
So just put the value of i as 1 to 9 and check the value at which the value of d is a perfect integer i.e. d must be completely divisible by ‘e’.
d = ((96 * 1)+ 1 ) / 5 = 19.4
d = ((96*2)+1) / 5 = 38.6 , d = ((96*3) +1)/ 5 = 57.8
d = ((96*4)+1) / 5 = 77
So at i = 4 we got value of d as perfect integer . Hence d = 77 (decryption key)
Step 6 : Now the Public key = (e, n) = (5, 119)
And , the Private key = [d, n] = (77, 119)
Step 7 : Calculate cipher text message for given plain text message m = 10.
Plain text denoted as p = 10 (m denoted as p)
C = P^e mod n = 10^5 mod 119 (value of e calculated above)
It can be represented as
= 10^5 mod 119 = [1000 mod 119] *[100 mod 119] mod 119
100^5 mod 119 = [10^3 mod 119] *[10^2 mod 119] mod 119
C = P^e mod n = 100000 mod 119 = 40
Step 8 : Now calculate plain text P required at the time of decryption. Once sender sends 40 to the receiver then receiver can calculate plain text p.
P = C^d mod n
= 40^77 mod 119
Now represent 40^77 mod 119 as mention above it will results p as 10.
Because decryption process always yields original message (plain text)
P = 40^77 mod 119 = 10
Thus we successfully able to decrypt the original plain text as given initially by the sender using the RSA algorithm
Limitations Of RSA Method
Although RSA can be used to encrypt and decrypt actual messages, it is very slow if the message is long. RSA, therefore, is useful for short messages such as a small message digest or a symmetric key to be used for a symmetric-key cryptosystem.
Possible Attacks In RSA Method Of Cryptograthy !!
Although RSA is a mush secure encryption method, still some attacks are possible :
Brute force attack : Hacker tries all possible private keys.
Mathematical attacks : Hackers attacks on n i.e. tries to factorize the product of two
prime numbers.
Tuning attacks : It totally depends on the running time of the decryption algorithm.
Chosen Cipher text attack : Hacker tries to attack the properties of RSA algorithm
RSA process is very widely used for the digital signature based authentications. Hope you really liked this post. Stay tuned for more interesting stuff in this series .

Aric is a tech enthusiast , who love to write about the tech related products and ‘How To’ blogs . IT Engineer by profession , right now working in the Automation field in a Software product company . The other hobbies includes singing , trekking and writing blogs .





