Basics of Elliptical Curve Cryptography !! (The Ultimate Guide)

Till now we have learned about the key-based encryption and decryption modes in the cryptography process in symmetric and asymmetric types . Now Elliptical Curve Cryptography is the enhanced and more efficient (more fast and secure) way of cryptography indeed. We will explore ECC in detail here,so just sit back and read further .  

Elliptic Curve Cryptography (ECC) is evolved as an alternative to traditional public-key cryptosystems like Rivest Shamir Adelman, Digital Signature Algorithm and Diffie Hellman. Elliptic Curve Cryptography provides equivalent security with smaller key size i.e. 160-bits whereas RSA uses 1024 bits .

ECC results in faster computations, lower power consumption, as well as it saves memory and bandwidth utilization. ECC was developed by Neal Koblitz and Victor S. Miller in 1985 which use the elliptic curves in cryptography.

What Is Elliptic Curve Cryptography (ECC) ?

The Elliptic curve cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. Since 1985, ECC has received intense scrutiny from cryptographers, mathematicians, and computer scientists around the world.

In ECC there is a no significant weaknesses have been found and it also achieves the high confidence in the security of ECC. ECC becomes more powerful and attractive rather than RSA and DSA. Top standard agencies such as ANSI, IEEE and ISO certified that ECC has been gaining popularity
over past few years.

An elliptic curve is the set of solutions of an equation of the form :

y^2 = x^3 + ax + b  , Where the coefficeints a and b are elements of the field.

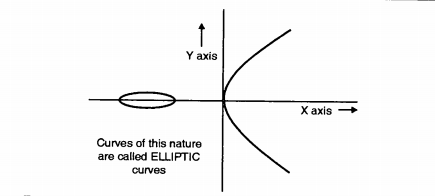
Each value of the ‘a’ and ‘b’ gives a different elliptic curve. An equation of this kind can be studied over various mathematical structures, such as a ring or a finite field.

One interesting property of the elliptic curve is that it forms a group that enables us to do Cryptography. The public key is a point in the curve and a private key is a random number as shown in the below figure .

The public key is obtained by multiplying the private key with the generator point G in the curve. 

Elliptic Curve Cryptography Encryption And Decryption Process !!

There are several methods to perform ECC Encryption and Decryption following method is one of them.

The first task in this system is to encode the plaintext message ‘m’ to be sent as an x-y point Pm.

It is the point Pm that will be encrypted as ciphertext and subsequently decrypted. Note that we cannot simply encode the message as the x or y coordinate of a point, because not all such coordinates are in Ep(a, b). Where Ep (a,b) is coordinate representing the group elements of the message .

The Ep(a, b) denotes the elliptic group mod p whose elements (x, y) are pairs of nonnegative integers less than p satisfying the following equation;

y^2 = x^3 + ax + b (mod p)

Where a and b is non negative integers, less than p that satisfy the following equation:

4a^3 + 27b^2 . (mod p) 9 ≠ 0

An encryption/decryption system requires a point G and an elliptic group Ep(a, b) as parameters. Each user A selects a private key Ar and generates a public key Pu = Ar xG. 

To encrypt and send a message Pm to B, A chooses a random positive integer x and produces the cipher text Cf consisting to the pair of points
Cf = {xG, Pm + xPb}

Here, A has used B’s public key Pb. To decrypt the ciphertext, B multiplies the first point in the pair by B’s secret key and subtracts the result from the second point:
Pm + xPb – Br (xG) = Pm + x(BrG) – Br(xG) = Pm

A has masked the message Pm by adding xPb to it. Only A knows the value of x, so even though Pb is a public key, nobody can remove the mask xPb.

However, A also includes a “clue,” which is enough to remove the mask if one knows the private key Br. For an attacker to recover the message, the attacker would have to compute X given G and xG, which is hard.

Hope you really liked this post about Elliptic Curve Cryptography. Stay tuned for more interesting stuff in this series .