Control System – Root Locus Method

July 1, 2018June 18, 2020 Techie Aric 0 Comments

Spoiler : This post will be long yet interesting!!

In my previous post , we have seen the Routh Hurwitz criterion in detail. It gives us the information about the number of poles in the right half of the s-plane for an unstable system and position of poles in the imaginary axis in case of a marginally stable system. Thus the major shortcoming of the Routh criterion is that it doesn’t give us the remaining pole location.

Root Locus , introduced by W.R . Evans is a pictorial representation of how ‘closed loop poles’ move when the gain of the system is varied. This technique is extensively used in control engineering as it gives the entire dynamic response of the system.

The main advantage that is most important of root locus is to verify the system behavior by setting the value of the gain ‘K’ . The adjustment into the value of ‘K’ will consequently trace the origins of roots on the R-H plane..

Angle and Magnitude Condition

These are the two important conditions that we would need to know before we can proceed. We know the characteristic equation is given by:

1 + G(s)H(s) = 0

G(s)H(s) = -1 ,

As the s plane is complex , we can write

G(s)H(s) = -1 + 0j

This equation has magnitude as well as phase,

| G(s)H(s) | = |-1 + 0j | = 1 ,

∠ G(s)H(s) = $\pm$ 180 $^{\circ}$ , but since -1 + 0j point can be traced with an angle of $\pm$ 180 $^{\circ}$

$\pm$ 540 $^{\circ}$

, $\pm$ 900 $^{\circ}$ …… we thus have a generalized angle condition as :

∠ G(s)H(s) = ( 2q + 1 ) 180 $^{\circ}$ q = 0 , 1 , 2 ………….

Construction of Root Locus(General method for drawing)

We construct root locus by following a certain set of rules. Implementing each of the below-mentioned rules gives us the final root locus.

Rule no.	Statement	Comments
Rule 1	The root locus is symmetric about the real axis	Root locus that we construct will always be symmetric about the real axis (irrespective of system)
Rule 2	Total number of loci	The total number of loci will be equal to max(p,z) where p is no: of the open loop poles and z is number of open loop zeros
Rule 3	Real axis loci	A point that lies on real axis basically lies on the root locus only if the total number of real open loop poles and open loop zeros present in the RHS of this point is odd
Rule 4	Angle of asymptotes	Total number of branches of the root locus tending towards infinity is equal to p – z. The angle of asymptotes gives us the direction along which these p-z branches approach infinity.
Rule 5	centroid	Centroid is a point on real axis , through which the asymptotes pass.
Rule 6	Breakaway point	A break away point on the root locus is a point where the two poles will meet. Once they meet,they divide (split) i.e break away from the real axis.
Rule 7	Angle of departure / arrival	This gives us angles along which complex poles will depart( and complex zeros arrive) from their original position
Rule 8	Intersection with the imaginary axis	This gives us points on imaginary axis which the given root locus cut through while moving to right half of the s plane

We shall take a simple example and explain each rule ,

Let G(s)H(s) = $\frac{k(s+6)}{s(s+2)(s+5)}$ , H(s) = 1

Rule 1 : The root locus is symmetric about the real axis

Irrespective of the system, the root locus that we construct will always be symmetric about the real axis.

Rule 2 : Total number of loci

The total number of loci will be equal to max(p,z) where p is no: of the open loop poles and z is number of open loop zeros.

Total number of branches of the root locus tending towards infinity is equal to p – z

In this case we have, G(s) = $\frac{k(s+6)}{s(s+2)(s+5)}$ , H(s) = 1 p = 3 , z = 1

Total number of loci = max ( p , z ) = max ( 3 , 1 ) = 3

Total number of loci tending to infinity = p – z = 3 – 1 = 2

All branches of the root locus start from open-loop poles . In the given example , of the 3 loci, 2 will go to infinity , while one of them will go to the zero.

Rule 3 : Real axis loci

Any point on the real axis will lie on the root locus only if the total number of real open loop zeros and the open loop poles to the right-hand side of the given point is odd

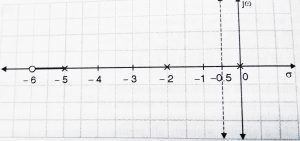
We plot the open loop poles and zeros in the s-plane first:

In this consider any point ‘a’ between 0 and -2. Total number of real poles and zeros on right of this point is odd.(only 1 pole ).

Now similarly consider another point ‘b’ in beween -2 and -5 . Total number of real poles and zeros to the right of this point is even(two poles) .

Hence this point doesn’t lie on root locus. Applying the same principles we can state that points lying between -5 and -6 will be a part of root locus.

Rule 4 : Angle of asymptotes

Total number of branches of the root locus tending towards infinity is equal to p – z. The angle of asymptotes gives us the direction along which these p-z branches approach infinity.

Angle of asymptotes is given by the formula

${ \beta }_{ x }\quad =\quad \frac { (2x-1)180^{ \circ } }{ p-z }$ where x = 0 , 1 , 2 , 3 ……p-z-1

In the given example G(s) = $\frac{k(s+6)}{s(s+2)(s+5)}$ , H(s) = 1 Here p = 3 , z = 1

Total number of branches approaching infinity are= p – z = 3 – 1 = 2

Hence ${ \beta }_{ 0 }\quad =\quad \frac { (2\times0-1)180^{ \circ } }{ 2 }$ = 90 $^{ \circ }$ , ${ \beta }_{ 1 }\quad =\quad \frac { (2\times1-1)180^{ \circ } }{ 2 }$ = 270 $^{ \circ }$ ,

Rule 5 : Centroid is a point on real axis , through which the asymptotes pass.

${ \sigma }_{ c }=\quad \frac { \sum { (Real\quad parts\quad of\quad poles\quad of\quad OLTF) } \quad -\quad \sum { (Real\quad parts\quad of\quad zeros\quad of\quad OLTF) } }{ p-z }$

Where ‘OLTF’ is Open loop transfer function

The centroid is always real and it may or may not be part of root locus.In this example,

G(s) = $\frac{k(s+6)}{s(s+2)(s+5)}$ , H(s) = 1 Here p = 3 , z = 1 ,

$\sum { (Real\quad parts\quad of\quad poles\quad of\quad OLTF) }$ = 0 – 2 – 5 = – 7

$\sum { (Real\quad parts\quad of\quad zeros\quad of\quad OLTF) }$ = -6

Hence , ${ \sigma }_{ c } = \frac{-7-(-6)}{2} = \frac{-1}{2}$

Once centroid is obtained , we draw the asymptotes passing through this centroid.

Note: Asymptotes only gives us direction . It is not final root locus and hence should be drawn with light pencil (or dotted line)

Rule 6 : The Break away point

A break away point on the root locus is a point where the two poles collide (meet) .Once they meet ( or collide),they divide (split) that is break away from real axis.

We have to follow following steps for finding out the break away point,

Compute the characteristic equ.
Write it in terms of k
Compute 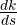$\frac{dk}{ds}$ and equate to 0.

Now let’s take our example,

G(s) = $\frac{k(s+6)}{s(s+2)(s+5)}$ , H(s) = 1 Here p = 3 , z = 1

Step 1: Characteristic equation : 1 + G(s)H(s) = 0 ,

We get , s(s + 2) (s + 5) + k(s + 6) = 0

Step 2: We write this equation in terms of k

k = $\frac{-s(s+2)(s+5)}{s+5}$ = $\frac{-s^{3}-7s^{2}-10s}{s+6}$

Step 3: Compute $\frac{dk}{ds}$ = 0

$\frac{d}{ds}(\frac{-s(s+2)(s+5)}{s+5})$ = 0

We use $d(\frac{u}{v})$ rule , d( $\frac{u}{v}$ ) = $\frac { v\dot { u } \quad -\quad u\dot { v } }{ { v }^{ 2 } }$ (division rule of derivatives)

$d(\frac{u}{v}) = \frac{d}{ds}(\frac{-s^{3}-7s^{2}-10s}{s+6})$ = $\frac{(s+6)(-3s^2-14s-10)-(-s^3-7s^2-10s))}{(s+6)^2}$ = 0 ,

On solving we get,

2 $s^3$ + 25 $s^2$ + 84s + 60 = 0 ,

The roots of this equation are -0.9753, -4.1988 , -7.32

Breakaway points are points where two poles come and meet. Hence breakaway point have to lie on the root locus . Out of three root, only -0.9753 lies on real axis of the root locus(see rule number 3)

Rule 8 : Intersection with the imaginary axis(we will see rule 8 first and then rule 7 will be explained)

This provides us the points that lies in the imaginary that the root locus cut through while moving towards the right half of s plane.

For the intersection with the imaginary axis, we follow the following steps:

Consider characteristic equation 1 + G(s)H(s) = 0,
Construct Routh array
Determine 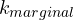$k_{marginal}$ ( row of zeros)
Then obtain the Auxiliary equation
Finally find the roots of the Auxiliary equation. These will give the intersection points with the imaginary axis .

Let’s take our example,

G(s) = $\frac{k(s+6)}{s(s+2)(s+5)}$ , H(s) = 1 ,

Characteristic equation = 1 + G(s) H(s) = $s^3$ + 7 $s^2$ + (10+ k)s + 6k = 0

We now construct Routh array,

$s^3$	1	10 + k
$s^2$	7	6k
$s^1$	$\frac{7(10+k)-6k}{7}$	0
$s^0$	6k

Now for poles to lie on imaginary axis, the system has to be marginally stable. For marginal stability one row of the routh array must be zero.Thus we take one row zero as:

$\frac{7(10+k)-6k}{7}$ = 0 ,

On solving, $k_{marginal}$ = -70 ,

Now we know ‘k’ is the gain of the system, so it can’t be negative.

Thus , k = -70 cannot be true, hence there is no ( i.e there is no intersection with the imaginary axis and the two poles will collide at breakaway point and do not move towards the right half plane).

Rule 7 : Angle of departure/arrival

This gives us angles along which complex poles will depart( and complex zeros arrive) from their original position.

This rule is used only if the system has complex pole or zero. Since our example had only real poles and zero, we should take new example to compute the angle of departure/arrival, consider a system having

G(s) = $\frac{k(s+4)}{s(s+1+j)(s+1-j)}$ , H(s) = 1

Given system has complex pole and thus we need to use rule 7. The root locus arrives at a complex zero while a root locus departs from a complex pole i.e Angle of departure is associated with complex poles while angle of arrival is associated with complex zeros. We encounter complex poles more often and hence angle of departure is what we need to use more often. Angle of departure ( ${ \Phi }_{ D }$ ) is given by the formula:

${ \Phi }_{ d }$ = 180 – ${ \Phi }$ ,

Where ${ \Phi }$ = $\sum { Angles\quad made\quad by\quad poles } \quad - \quad \sum { Angles\quad made\quad by\quad zeros }$ ,

Similarly Angle of arrival is given by , ${ \Phi }_{ A }$ = 180 + ${ \Phi }$

We use graphical method to compute ${ \Phi }$ . We join all poles and zeros to the complex pole whose angle of departure needs to be calculated. We then compute the angle made by poles and angles made by zeros. Let’s take our example,

G(s) = $\frac{k(s+4)}{s(s+1+j)(s+1-j)}$ , H(s) = 1 ,

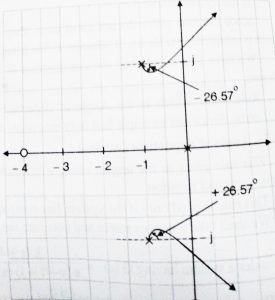
We plot the open loop poles and zeros, we join all remaining poles and zeros to this complex pole.

${ \Phi }_{ p1 }$ = 135 $^{ \circ }$ , ${ \Phi }_{ p2 }$ = 90 $^{ \circ }$ , ${ \Phi }_{ z1 }$ = $\tan ^{ -1 }{ (\frac { 1 }{ 3 } ) }$ = 18.43 ,

${ \Phi }$ = $\sum { Angles\quad made\quad by\quad poles } \quad \quad -\quad \quad \sum { Angles\quad made\quad by\quad zeros }$ ,

Hence , ${ \Phi }$ = ${ \Phi }_{ p2 }$ + ${ \Phi }_{ p1 }$ – ${ \Phi }_{ z1 }$ = 225 – 18.43 = 206.57 ,

${ \Phi }_{ D }$ = 180 – ${ \Phi }$ = -26.57 $^{ \circ }$ ,

Hence the Angle of departure is -26.57 $^{ \circ }$ ,

What is the significance of this angle?

This means that the complex pole at s = -1 + j will depart from its original position at an angle of -26.57 $^{ \circ }$ and then intersect the imaginary axis at a value obtained in rule 8. Angle of departure of other complex pole at s = -1 – j will be 26.57 $^{ \circ }$ as shown below,

Determining the value of ‘k’ from the Damping Ratio (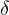 $\delta$ ):

We already saw the concept of damping in my time response analysis post.The damping ratio is controlled by dominant roots.Now to determine the value of ‘k’ we may use the following steps:

Draw Root locus
Given 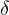$\delta$ , compute $\theta = \cos ^{ -1 }{ \delta }$ ,
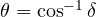Draw a line having angle 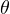$\theta$ from origin such that 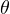$\theta$ is measured from the negative real axis.
Identify the point at which this line intersects the root locus, let it be point s = -a + bj .
Put this value of s in the magnitude condition , |G(s)H(s)| = 1 and get the value of ‘k’

Thus it is indeed clear that the root locus method is to evaluate the variation of the poles of the CLTF (closed loop transfer function) with respect to control gain (k) of the system .

If we can solve the characteristic equation of the closed-loop system, then we can directly plot this variation and there is no need for the root locus method.

However for larger order characteristic equations, it is usually difficult to factor the polynomials. It is here that the root locus method comes in.

In my next post , I will be giving all varieties of numerical that you can expect from this topic. So again go through and learn all the rules and concepts from this post, meet you soon in my next post.

Techie Aric

Aric is a tech enthusiast , who love to write about the tech related products and ‘How To’ blogs . IT Engineer by profession , right now working in the Automation field in a Software product company . The other hobbies includes singing , trekking and writing blogs .

Spread the Wisdom !!

Angle and Magnitude Condition

Determining the value of ‘k’ from the Damping Ratio ():

Techie Aric

You May Also Like

Leave a Reply Cancel reply

Determining the value of ‘k’ from the Damping Ratio ( $\delta$ ):