Control system – Solved examples of Mason’s Gain Formula

As we know practice indeed is the key to success, so you should practice a lot these concepts from reputed books to brush up your solving skills. In this post , we will be continuing with our previous post concept i.e ‘Mason’s Gain Formula’ (application part).

So before we start , I hope you already learned all the terms(from my previous post) that we will be extensively using here to solve questions.So let’s proceed,

We  have mainly three different variety of questions(related to this topic) i.e:

Application of Mason’s Gain Formula when:

• Block diagram (or Signal Flow graph) is given and we need to find the overall transfer function
• Solving Signal flow graph when equations are given
• Electrical networks are given

So let’s have a look into these three sections one by one.

We already know how to deduce signal flow graph from any block diagram model. Let us see how Mason’s Gain Equation works now :

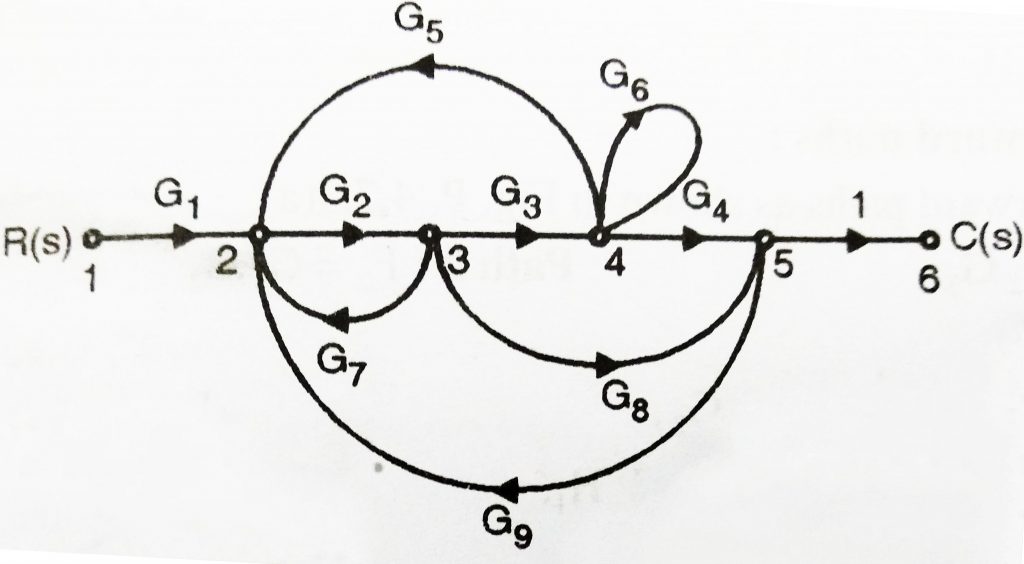
Here we want to obtain transfer function for the following signal flow graph

Now we have to follow our steps as given in my previous post,

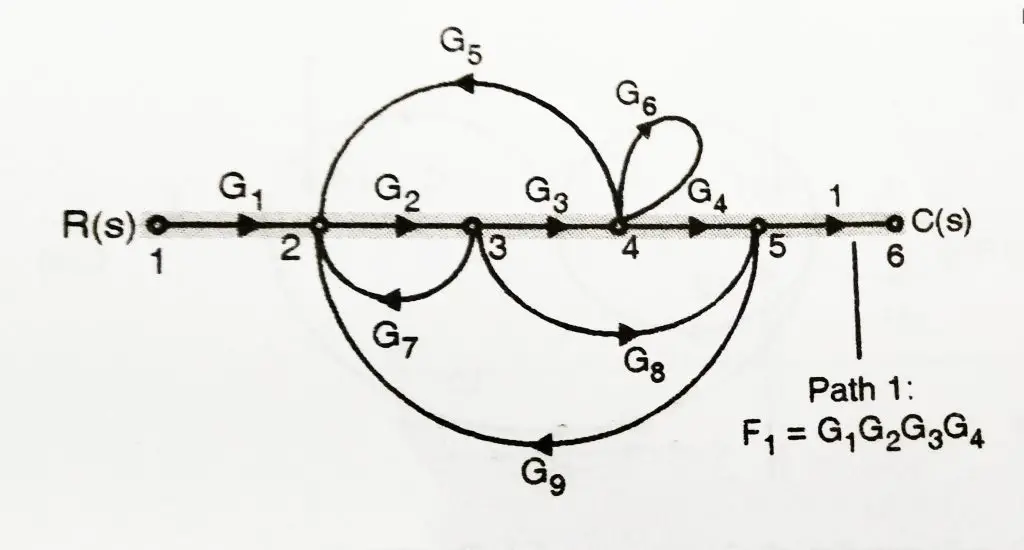
Step 1: Obtain Forward path

From the flow graph, we can observe that in total two forward paths present i.e 

     

 

Step 2 : Total number of loops

Now , as we already found our required forward paths, we require a total number of loops.

There are total 5 loops in the signal flow graph if you observe carefully.

  = 

  ,

  =  ,

  =  ,

  =  ,

  =  ,

Step 3 : Total number of 2 non touching loops:

  =    =   

Step 4 : There are no three non touching loops.

Step 5 : Value of  Δ 

Δ  =  1  –    +   

hence,  Δ =  1 –   

Step 6 : Find out the value of    and     :

All the loops touch the forward path

Thus ,     =  1

Loop   doesn’t touch the forward path

Thus,   =  1  –    =  (1 –)

Now the overall transfer function using Mason’s Gain formula can be given by :

TF  =   C/R   = 

   

You may refer below figure to make your understanding explicit about the 5 loops , we have been working with .

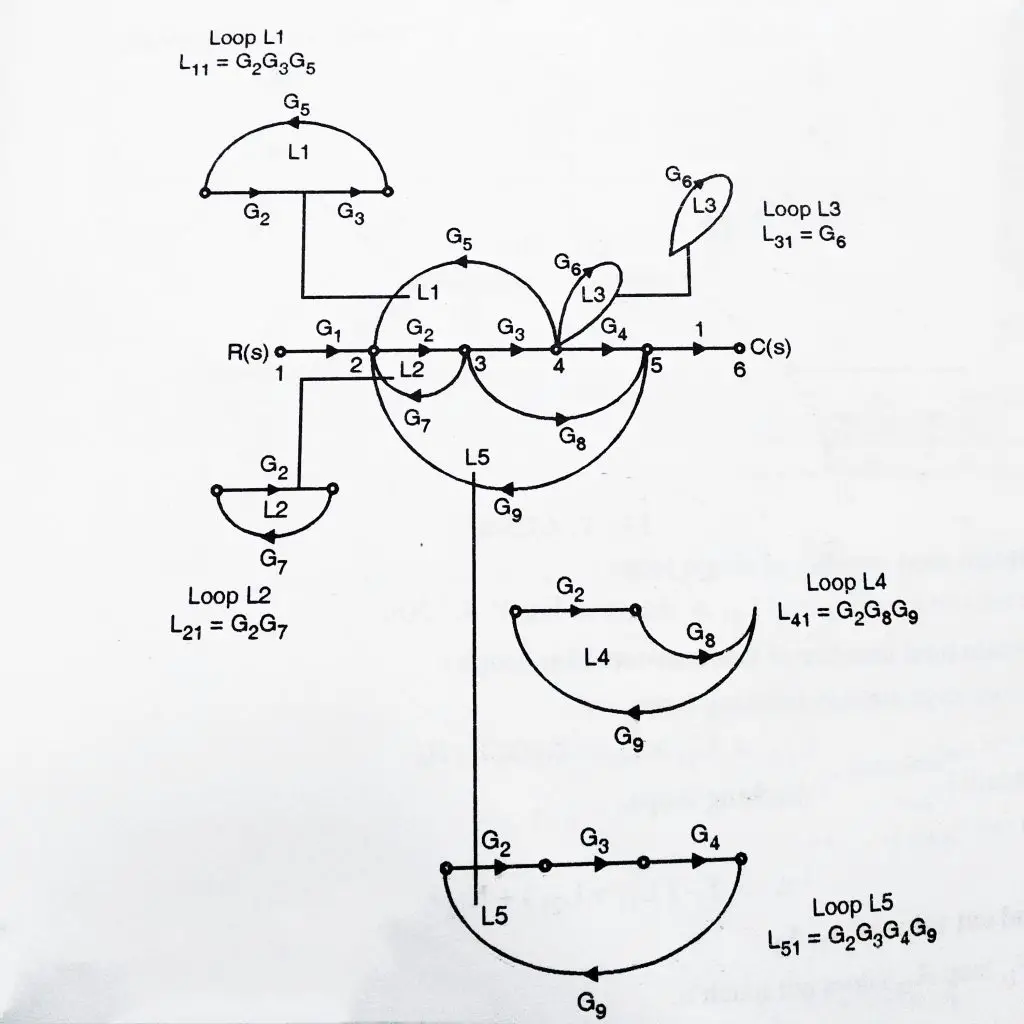
Here comes the end of our first variety, i.e deducing transfer function from a given signal flow graph. Now we proceed further to the second and third variety.(Both this can be termed as subset of first variety as for both of these , we need to deduce the signal flow graphs first , then we have to follow the normal steps as we followed in first variety).

If  a block diagram is given to us, then we must first deduce the signal flow graph as shown below:

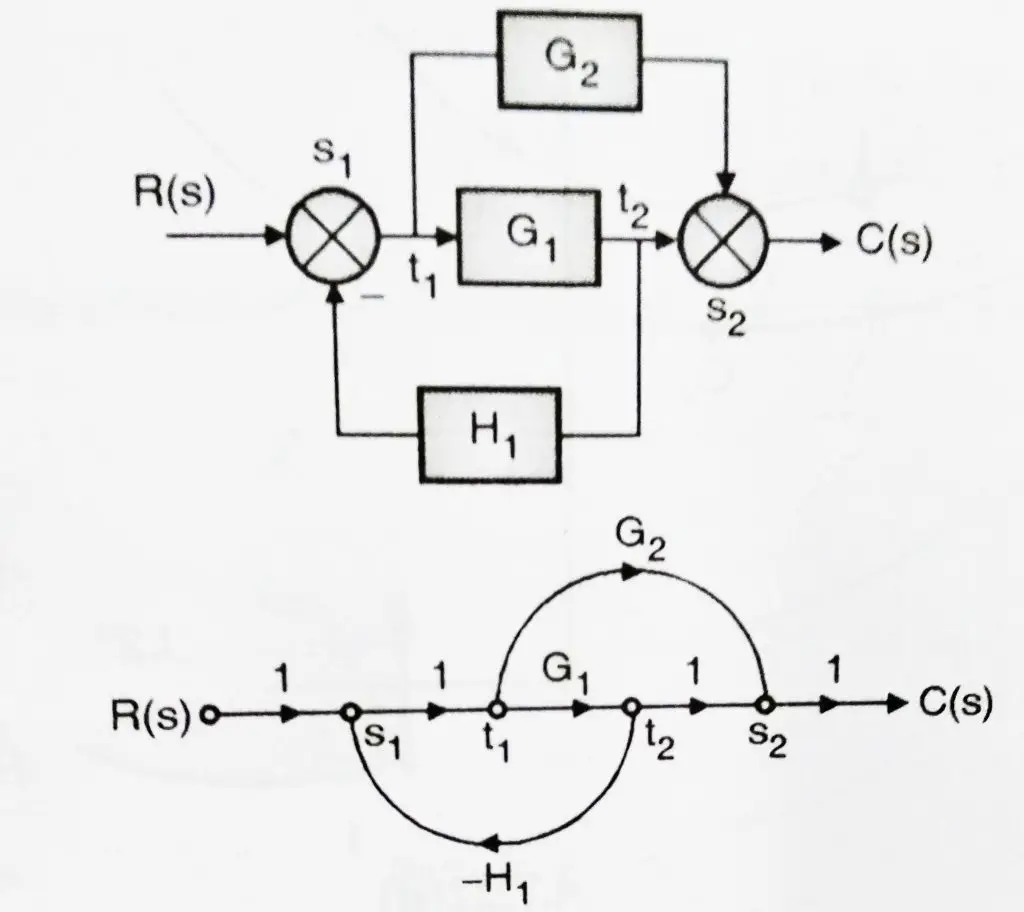
Step 1 : Obtain forward paths :

There are two forward paths

=       and       = 

Step 2 : Obtain total number of single loops:

=  –

Step 3 : Obtain number of two non touching loops:

There are no two non touching loops.

Step 4 : Find the value of  Δ :

             Δ =  1 –  =  1  – 

Step 5 : Find the value of     and 

Since the loop   touches as well as .

Thus,          =  1  ,    =  1

Step 6 :  Using mason’s Gain formula, we have :

TF =  C(s)/R(s)  = 

TF =    

Now let us see the last variety of numerical in this topic:

Suppose the equations given as 

;

;

;

There are  four nodes , , and . we shall now draw the signal flow graph using above equations:

Step 1 : Obtain the number of forward paths:

Step 2 : Obtain total number of loops

         ;                ;

Step 3 : Obtain number of non touching loops

There are no two  non touching loops 

step 4 : Find out the value of Δ :

Δ  =  1 –               ;                           Δ  =  1 –     ;

Step 5 : Find out the value of  :

Since the two loops touch all four forward paths,

Thus =  1

Step 6 : Using Mason’s Gain formula, we obtain transfer function :

   

Finally we reach the end of this post. Later , i will  give more solved examples PDF with this post. I request you to go through the questions first (without looking into the solutions), after trying from your end , verify the solution given in the end of the document.Stay tuned for the next important ( and interesting) topic of this subject in my next post.