Control System – Solved Example of Block Reduction Technique

You must have already learnt all the basic rules for reducing any complex block diagram. So now we need to implement those rules and will see how actually block diagram reduction technique works. You may take help from some other standard books in Control System, to practice more numerals to make this topic easy. In this post  , every step will be associated with reference figure to make you understand the rules in lucid manner. I request you to go through the questions first (without looking into the solutions), after trying from your end , verify the solution given.

Refer the below diagram, we are interested to find the ratio of  C(s)/R(s)  (overall transfer function of the system)

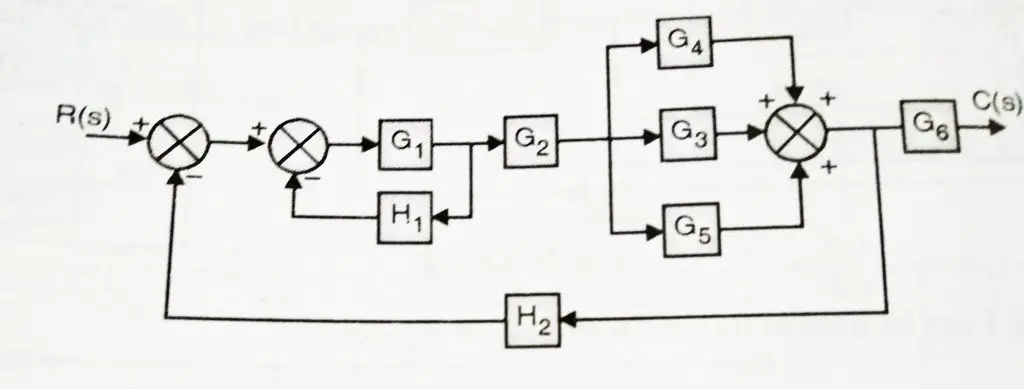
Now we should apply various rules we learnt in my previous post to solve this complex block diagram.From given block diagram, clearly blocks G4, G3 and G5 are in parallel. So we should apply rule 2 first(refer below figure)

Now blocks G2 and G3 + G4 + G5 are in cascade(series), so we should now apply rule 1 to get G2 and (G3 + G4 + G5) resultant .(refer below figure)

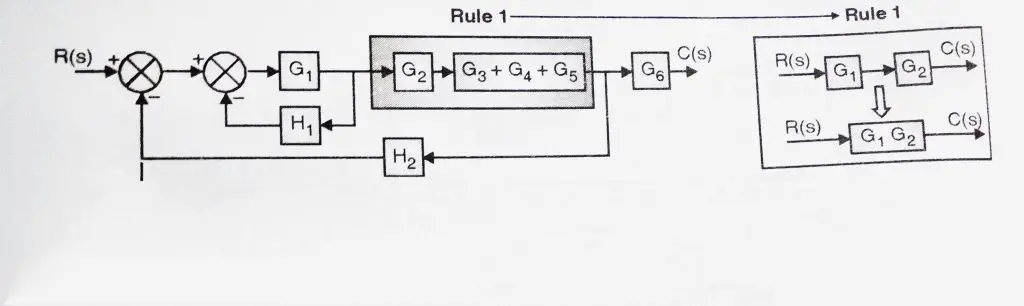
 3.  Now rule 3 can be applied to feedback loop G1-H1 . This is shown in below figure:

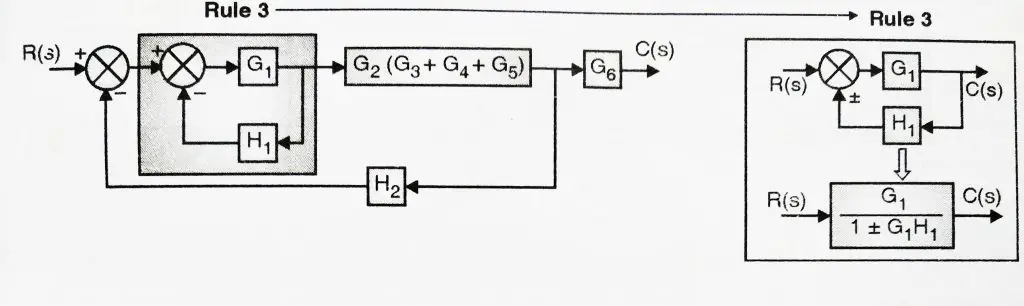
4.  Now rule  1 can be used on cascade blocks(which are in series) in forward path      and    G2 (G3 + G4 + G5).You may refer below figure:

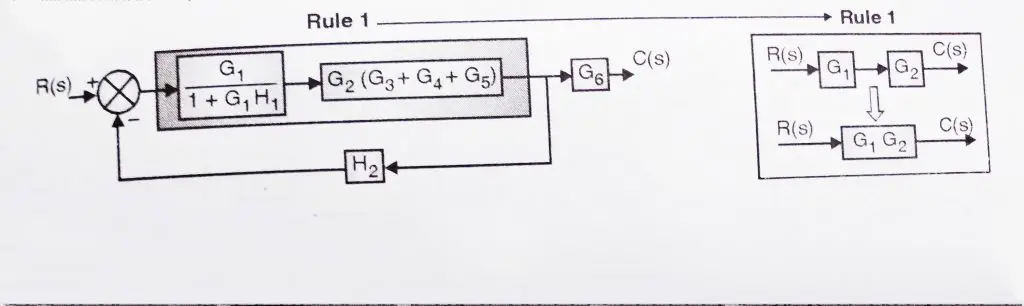
5.  Now we can use rule 3 on the loop containing feedback block.

We can now use rule 3 where   and H(s)  =  H2

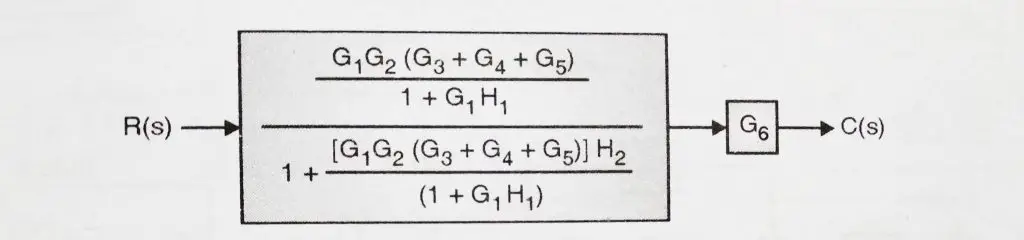
6.  Finally we ave to apply rule 1, (as we now left with G6 block in series with the resultant block diagram). Simplified block diagram can be shown below:

After applying rule 1, we will get:

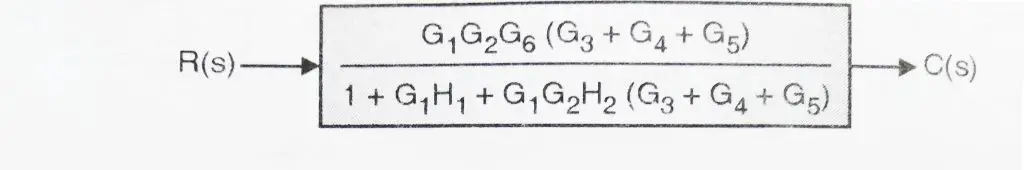
So, from above example it is very much evident that, using block reduction rules we can easily reduce complex block diagram system into simple block diagram system. Stay tuned for more interesting topics in the next posts.