Control System – Transient time response of a Second order (Underdamped) System with 0 < δ(damping ratio) < 1

June 24, 2018June 17, 2020 Techie Aric 0 Comments

Spoiler : This post will be a little difficult to understand at first. I request you to go through some standard books too for the derivations part for reference. Lastly, be patient and enjoy the post !!

In my previous post, we have seen Time response for First order system and also the general second-order Closed loop transfer function. Now in this post we shall look into the time response of Second-order system(mainly the underdamped system).

Before that, we should recap the important types that we covered in my previous post i.e different types of systems (based on the value of ‘Damping factor’).You may refer below diagram for your ready reference:

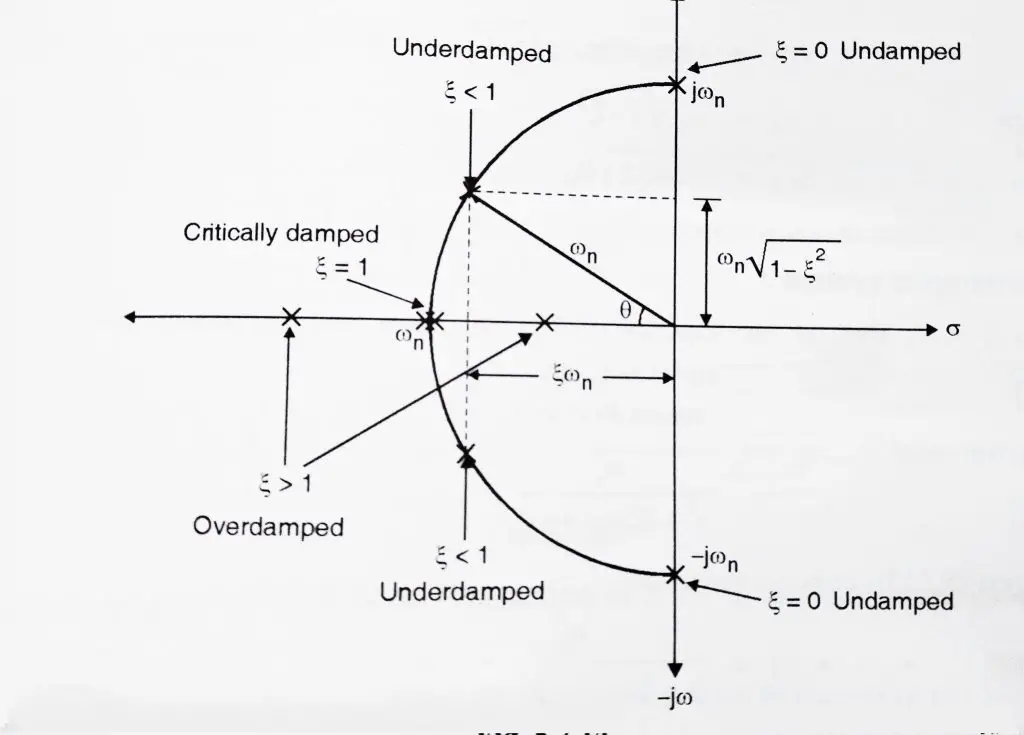
In the above figure damping ratio ( $\delta$ ) has been represented as $\xi$ .

Of all the four cases of damping, the most important is when 0 < $\delta$

< 1 i.e the ‘underdamped’ system type. We must understand the ‘Underdamped System’ very well. We now study the behavior of a 2nd order underdamped system when subjected to unit impulse and unit step input as input.

Derivation of Unit Impulse Response of a 2nd order ‘Underdamped’ System:

The standard second order transfer function is given by:

$\frac{C(s)}{R(s)} = \frac { { { \omega }_{ n } }^{ 2 } }{ s^{ 2 } + 2\delta \omega_{ n }s + { { \omega }_{ n } }^{ 2 } }$

The poles can be obtained by equating denominator term to zero.

${ s^{ 2 }+2\delta \omega _{ n }s+{ { \omega }_{ n } }^{ 2 } }=0$

The poles can be given by

$s_{ { 1 },{ 2 } }=\quad -\quad\frac { \quad 2\delta { \omega }_{ n }\quad \pm \quad \sqrt { 4{ \delta }^{ 2 }{ { \omega }_{ n } }^{ 2 }\quad -\quad 4{ { \omega }_{ n } }^{ 2 } } \quad }{ 2 }$

$s_{ { 1 },{ 2 } }=\quad -\frac { \quad 2\delta { \omega }_{ n }\quad \pm \quad \sqrt { (-4{ { \omega }_{ n } }^{ 2 })\quad (1\quad -\quad { { \delta }_{ n } }^{ 2 }) } \quad }{ 2 }$

Let us assume, $\omega_{ d }=\omega_{ n }\sqrt { (1\quad -\quad { { \delta } }^{ 2 } }$

Then we have, $s_{ 1,2 }=\quad -\delta { \omega _{ n } }\quad \pm \quad j{ \omega _{ d } }$

Now we shall consider an underdamped system ( $\delta$ < 1),

When $\delta$ < 1, we will have complex roots. Also R(s) will be 1 as we are considering unit ‘impulse input’.

$C(s) = \frac { { { \omega }_{ n } }^{ 2 } }{ s^{ 2 } + 2\delta \omega_{ n }s + { { \omega }_{ n } }^{ 2 } }$ ( putting R(s)=1)

Above equation can be rearranged as ,

$C(s) = \frac { { { \omega }_{ n } }^{ 2 } }{ { (s+\delta \omega _{ n }) }^{ 2 }+{ { \omega }_{ n } }^{ 2 }(1-{ \delta }^{ 2 }) }$

Multiplying and dividing by ‘ ${ \omega }_d$ ‘ we get,

$C(s)=\frac { { { \omega }_{ n } }^{ 2 } }{ { \omega }_{ d } } \frac { { \omega }_{ d } }{ { (s+\delta \omega _{ n }) }^{ 2 }+{ { \omega }_{ n } }^{ 2 }(1-{ \delta }^{ 2 }) }$

But ${ { \omega }_{ n } }^{ 2 }(1-{ \delta }^{ 2 })={ { \omega }_{ d } }^{ 2 }}$

Hence, $C(s)=\frac { { { \omega }_{ n } }^{ 2 } }{ { \omega }_{ d } } \frac { { \omega }_{ d } }{ { (s+\delta \omega _{ n }) }^{ 2 }+{ { \omega }_{ d } }^{ 2 } }$

To obtain equation for c(t) we have to take Laplace Inverse of C(s),

We already know (from the inverse Laplace theory),

${ L }^{ -1 }\left( \frac { { \omega } }{ { (s+a) }^{ 2 }+{ \omega }^{ 2 } } \right) \quad =\quad (\sin { \omega t }). \quad { e }^{ -at }$

$L^{-1}[{C(s)}] = c(t) = L^{-1}[\frac { { { \omega }_{ n } }^{ 2 } }{ { \omega }_{ d } } \frac { { \omega }_{ d } }{ { (s+\delta \omega _{ n }) }^{ 2 }+{ { \omega }_{ d } }^{ 2 } }]$

Hence , $c(t) = \frac { { { \omega }_{ n } }^{ 2 } }{ { \omega }_{ d } }{ e }^{ -\delta { \omega }_{ n }t }\sin { { \omega }_{ d }t }$

${ { \omega }_{ n } }^{ 2 }(1-{ \delta }^{ 2 })={ { \omega }_{ d } }^{ 2 }}$

Then, ${ { \omega }_{ n } }\sqrt { (1-{ \delta }^{ 2 }) } ={ { \omega }_{ d } }$

Thus , $c(t)=\frac { { { \omega }_{ n } }^{ 2 } }{ { { \omega }_{ n } }\sqrt { (1-{ \delta }^{ 2 }) } } { e }^{ -\delta { \omega }_{ n }t }\sin { { \omega }_{ d }t }$

$c(t)=\frac { { { \omega }_{ n } } }{ \sqrt { (1-{ \delta }^{ 2 }) } } { e }^{ -\delta { \omega }_{ n }t }\sin { { \omega }_{ d }t }$

Under this condition , the system is called as underdamped system.

Derivation of Unit Step Response of a 2nd order ‘Underdamped’ System:

Now let us obtain response c(t) to a unit step input R(s)

We know for unit step input,

R(s) = 1/s

Hence $\frac{C(s)}{R(s)} = \frac { { { \omega }_{ n } }^{ 2 } }{ s^{ 2 } + 2\delta \omega_{ n }s + { { \omega }_{ n } }^{ 2 } }$

Underdamped case (0 < δ < 1) :

$C(s) = \frac { { { \omega }_{ n } }^{ 2 } }{{s} ({s^{ 2 } + 2\delta \omega_{ n }s + { { \omega }_{ n } }^{ 2 }}) }$ ( By putting R(s) = 1/s for step input)

This can be solved by using partial fractions. As $\delta$ in (0 < $\delta$ < 1), the roots of second-order transfer function will be complex. Also we will do some adjustments to solve the equations in an easier manner.

$C(s) = \frac { { { \omega }_{ n } }^{ 2 } }{(s) {s^{ 2 } + 2\delta \omega_{ n }s + { { \omega }_{ n } }^{ 2 }} }$

$C(s) = \frac { 1 }{ s } \quad -\quad \frac { s\quad +\quad 2\delta { \omega }_{ n } }{ { s^{ 2 }+2\delta \omega _{ n }s+{ { \omega }_{ n } }^{ 2 } } }$

$C(s) = \frac { 1 }{ s } \quad -\quad \frac { s\quad +\quad \delta { \omega }_{ n } }{ { { (s+\delta \omega _{ n }) }^{ 2 }\quad +\quad { { \omega }_{ d } }^{ 2 } } } \quad -\quad \frac { \quad \delta { \omega }_{ n } }{ { { (s+\delta \omega _{ n }) }^{ 2 }\quad +\quad { { \omega }_{ d } }^{ 2 } } }$

Where,

${ { \omega }_{ n } }^{ 2 }(1-{ \delta }^{ 2 })={ { \omega }_{ d } }^{ 2 }}$

then, ${ { \omega }_{ n } }\sqrt { (1-{ \delta }^{ 2 }) } ={ { \quad \omega }_{ d } }$

‘ $\omega_d$ ‘ is called the damped natural frequency and ‘ $\omega_n$ ‘ is called an undamped natural frequency. We can now use the Laplace transform, we then get,

${ L }^{ -1 }(\frac { { a } }{ { (s+a) }^{ 2 }+{ d^{ 2 } } } ) =\quad(\sin { dt }) { e }^{ -dt }$ ,

${ L }^{ -1 }(\frac { { s+a } }{ { (s+a) }^{ 2 }+{ d^{ 2 } } } ) =\quad (\cos { dt }) { e }^{ -dt }$ ,

Also, ${ L }^{ -1 }({\frac{1}{s}})= 1$ ,

Thus, in our case

${ L }^{ -1 }\quad \frac { s\quad +\quad \delta { \omega }_{ n } }{ { { (s+\delta \omega _{ n }) }^{ 2 }\quad +\quad { { \omega }_{ d } }^{ 2 } } } \quad = \quad (\cos { {\omega_d}t } ){ e }^{ -\delta{\omega_n}t }$ ,

${ L }^{ -1 }\quad [\frac { \delta { \omega }_{ n } }{ { { (s+\delta \omega _{ n }) }^{ 2 }\quad +\quad { { \omega }_{ d } }^{ 2 } } } ]=\quad \frac { { { \delta }{ \omega _{ n } } } }{ \omega _{ d } } { e }^{ -\delta { \omega _{ n } }t }(\sin { { \omega _{ d } }t })$ ,

${ { \omega }_{ n } }^{ 2 }(1-{ \delta }^{ 2 })={ { \omega }_{ d } }^{ 2 }}$

We can write the term , $\frac { { { \delta }{ \omega _{ n } } } }{ \omega _{ d } } = \frac { { { \delta }{ \omega _{ n } } } }{ { { \omega }_{ n } }\sqrt { (1-{ \delta }^{ 2 }) } } = \frac { { \delta } }{ { \sqrt { (1-{ \delta }^{ 2 }) } }}$ ,

Hence the total Laplace transform can be given by,

$c(t)=1-{ e }^{ -\delta { \omega _{ n } }t }\cos { { \omega }_{ d }t } -\frac { { \delta } }{ { \sqrt { (1-{ \delta }^{ 2 }) } } } { e }^{ -\delta { \omega _{ n } }t }\sin { { \omega }_{ d }t }$ ,

$c(t)=1-\frac { { e }^{ -\delta { \omega _{ n } }t } }{ { \sqrt { (1-{ \delta }^{ 2 }) } } } \quad ({ { \sqrt { (1-{ \delta }^{ 2 }) } \cos { { \omega }_{ d }t } }+(\sin { { \omega }_{ d }t } )\delta ) }$

Consider a right triangle such that,

Cos α = $\delta$ sin α = ${ { \sqrt { (1-{ \delta }^{ 2 }) } } }$

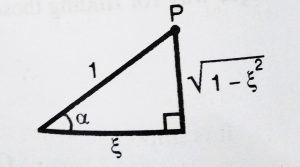
We have, sinA cosB + cosA sinB = sin (A + B)

on putting the required values we get,

c(t) = 1 – $\frac { { e }^{ -\delta { \omega _{ n } }t } }{ { \sqrt { (1-{ \delta }^{ 2 }) } } }$ sin ( $\omega_d$ t + α )

Also, we have tan α = $\frac { { \sqrt { (1-{ \delta }^{ 2 }) } }}{\delta} }$ thus, α = ${ \tan ^{ -1 }{{ \frac { { \sqrt { (1-{ \delta }^{ 2 }) } }}{\delta} } } }$

c(t) = 1 – $\frac { { e }^{-\delta { \omega _{ n } }t } }{ { \sqrt { (1-{ \delta }^{ 2 }) } } }$ sin ( $\omega_d$ t + ${ \tan ^{ -1 }{{ \frac { { \sqrt { (1-{ \delta }^{ 2 }) } }}{\delta} } } }$ ) ,

Above equation represents the solution for 0 < $\delta$ < 1 for the underdamped case. We can notice that the response contains a sine term multiplied by an exponential decaying term. Thus the final result will be sinusoidal decaying on an exponential envelope.

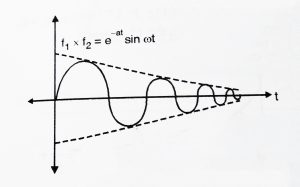
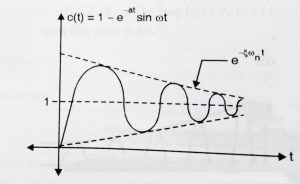
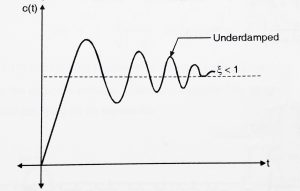
Some important points to be noted from the adjacent diagrams(refer both the figures),

1.We can see that response overshoots the reference and oscillate before settling to the final value.

Underdamped systems, thus exhibit overshoots and undershoots.

2. The pole location is in the 2nd and 3rd quadrants. Also the real part of poles generates the decaying exponential,while the imaginary part produces the sinusoidal function.

Before i end my post here, I want to leave you with one last thought, since we saw that the response characteristics contains overshoots and undershoots(also sometimes based lag before settling down) . So, there must be some well-defined parameters to understand the complete behavior of the response. Isn’t it ??……. (See you in my next post with the detailed explanation)

Techie Aric

Aric is a tech enthusiast , who love to write about the tech related products and ‘How To’ blogs . IT Engineer by profession , right now working in the Automation field in a Software product company . The other hobbies includes singing , trekking and writing blogs .

Spread the Wisdom !!

Techie Aric

You May Also Like

Leave a Reply Cancel reply