Area Of Triangle Formula For Equilateral , Scalen , With 3 Sides , Without Height etc – All Steps !!

In this post, we will be going to see different types of formulas for the area of triangle. We will see many types of cases through which you will be going to clear your concepts regarding all types of triangles. After learning all the concepts you will be able to solve many problems. These are going to super easy to understand. So, let’s get started.

How To Find Area Of Triangle ?

In order to find the area of triangle , we need to follow different formulas depending upon the various cases explained below :

• In a right-angled triangle, the area can be given simply by knowing the base and height of the triangle
• In a Scalen triangle, for the area we need all the sides of the triangle and then simply we can apply the Heron’s formula
• If two sides and an angle in between two sides given , then also we can find the area using trigonometry
• For an equilateral and isosceles triangle , we can directly give the area by knowing the side measures
• If we have coordinates of all the vertex , then we can find the area of a triangle using coordinate geometry

For all the above cases , we’ll now see the different formulas for finding the area of the triangle along with the examples for better understanding.

Type 1 : Area Of A Right Triangle Formula !!

This is the simplest way of finding the area in any right triangle using the formula given below . For this , we need to know the base and height of the triangle explicitly .

Also if anyone one of the side is not given , then we have to use the famous Pythagoras formula to find any required side :

We all know that the Pythagoras formula is :     (Hypotenuse)²   =    (Height)²    +      (Base)²

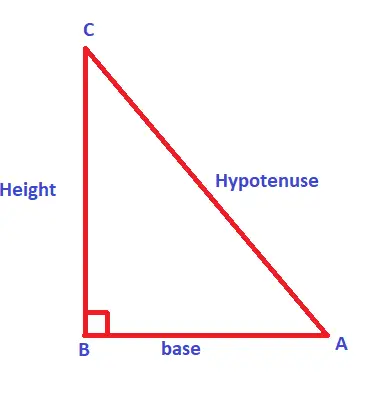
Case 1: Right Triangle With All Sides Known !!

If you are given an acute right-angled triangle will the two sides provided i.e. height and the base. Then you can easily calculate the area.

Area of the triangle is given by :

Area Formula :     1/2× base× height  =   (base × height) / 2

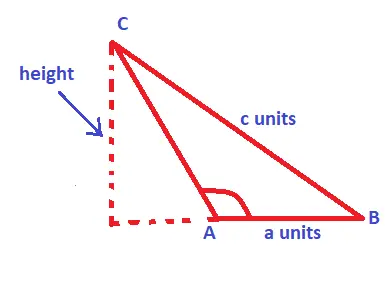
Case 2 : Area Of An Obtuse Angled Triangle !!

If you are given a triangle whose one angle is more than 90°. Here also you are given the height and the base but in this type of triangle, we will have to construct a height. Just extrapolate the base and join a line from a point. Then simply apply the same formula as above.

Area of triangle Formula :  1/2×base×height  =  (base × height) / 2

Now in the below figure, we can see a perpendicular line drawn from the point ‘C’ downwards to meet the extended line drawn from point ‘A’ . So we’ll get the height and the base is given as AB (a units). 

This same area formula can also be used for the area of Isosceles triangles as illustrated in the next section .

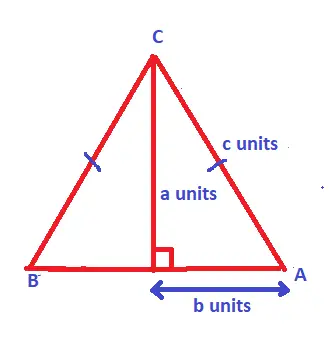
Type 2 : Area Of An Isosceles Triangle Formula !!

In an Isosceles triangle , always remember that two sides (and angles) will be equal . So for finding the area, we need to find the base and height precisely .

So now if you are given an isosceles triangle, where two sides are equal and provided all the sides are given . Here also you have to draw a height (a perpendicular line from C) by splitting right from the middle of the base .

In the above figure ,   measure of ‘b’  =   AB/2  

So, the base is divided equally. Now you can find the height by using the Pythagoras theorem i.e.
Formula:
Pythagoras formula:-    a² +b² = c²         (value of ‘a’ can be obtained from this)

Area of triangle   :-       1/2×base×height

Type 3 :  Area Of An Equilateral Triangle !!

Let’s say if you are given an equilateral triangle. In this triangle, we’ll have all three sides equal. Also, the angles will be equal and measure 60° .

Method 1 : For finding the area of this triangle, the method is the same as above. We’ll first draw a perpendicular line to the base for finding the height using the Pythagoras theorem.

Formula:      Pythagoras theorem    :-     a²  +b²  =  c²            where  b  =  AB/2  =  c/2   (AB = BC = CA = ‘c’)

Now the area can be given as :
Area of triangle   :-    1/2× base ×height

Method 2 : Whenever you are given an equilateral triangle, there is a simpler way to find the area. You have to use a formula and calculate it.

The formula for the area of an equilateral triangle :   √3/4 × (side)²

Here side is the measure of the side of an equilateral triangle . (AB = BC = CA And  ∠A  =  ∠B  =  ∠C  =  60° )

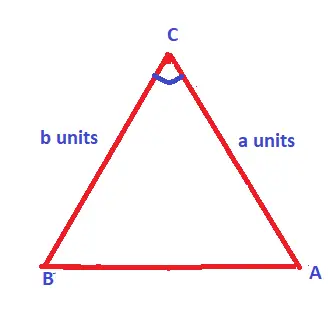
How To Find Area Of Triangle With Two Sides Given And Using Trigonometry !!

Now here , you will be given a triangle and two sides are given and an angle in the sequence: side – angle – side(SAS)

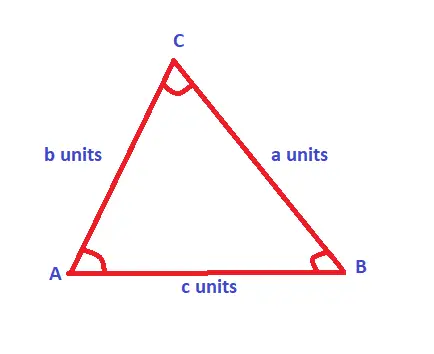
let us take the angles as A, B, C, and the sides are a,b,c. Here sides a and b are given and an angle C is given (in between sides a and b).

Area of triangle formula : 1/2 × a × b × Sin C  

How To Find Area Of Triangle With All Three Sides Given !!

Now if you are given a triangle with three given sides (SSS) .  Here you have to use Heron’s formula. Let the triangle has three sides a,b,c.  And are given.

Now here, first we need to find the Semiperimeter  ‘s’ = (a+b+c)/2    ;

Perimeter  of any triangle is simply given by  :   a + b + c   (where a,b and c are sides of the triangle)

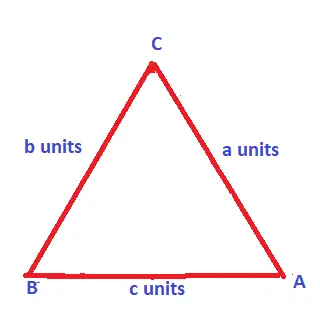
Finally, Area of triangle without height by Heron’s formula =

Hence if only sides are given , then also we can find the area by using Heron’s formula easily . 

How To Find Area Of Triangle Without Height Given ?

Now, this is interesting. What to do when we have no hieght is given. As seen above , if the height and base of a triangle known, then it’s pretty easy to find the area of the triangle.  But if we don’t have the height, then also finding the area is simple. 

In this case, we have to use Heron’s formula (if all the side i.e. SSS is known), and also if two sides are given and an included angle (SAS) given then we can directly use the trigonometry method seen above . 

For example, if two sides of a triangle are given as 8 cm and 4 cm respectively. Also, the included angle is given as 30° . Then find the area of the given triangle. 

Now here we are supposed to find the area of triangle without height.  So we have two adjacent sides and an included angle. Hence, the formula of the triangle is given as :

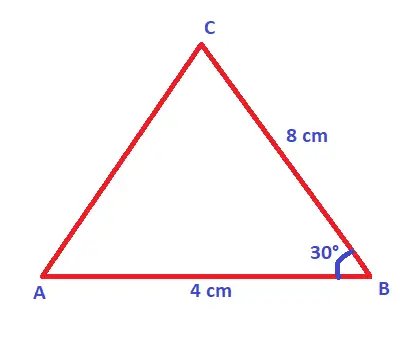
Area of Δ ABC  =  1/2  *  AB * BC *  sinB

we know that sinB =  sin30° = 1/2 =  0.5 

Thus the area is   =  1/2   *   4  *  8  *  0.5  =   8 sq cm

Now if all three sides are given and no height is present, we can quickly use Heron’s formula.

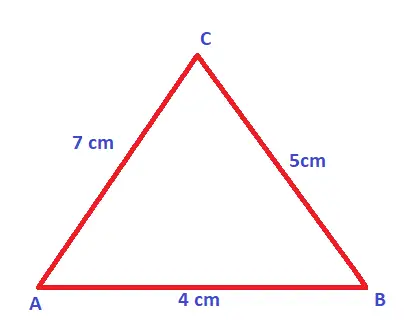
If three sides of a triangle are given as 4 cm, 7 cm, and 5 cm respectively. Then find the area of the given triangle. 

Now here we are supposed to find the area of triangle without height.  So we have all three sides  (SSS) and hence we can easily use Heron’s formula by first finding out the semi perimeter . Hence, the formula of the triangle is given as :

Semiperimeter  = ‘s’ =  (AB + BC + AC)/2   =    (4+5+7)/2 =  8 units

Area using heron’s formula will be =

where ,  AB = a ,   BC  = b   ,   AC  =  c    , now putting the side values as given above :

Area of  ΔABC  =       =    =   9.79 sq cm

 

How To Find Area Of Triangle Using Coordinate Geometry !!

In coordinate geometry, if we know the x-axis and y-axis coordinates for all the three vertices , then directly we can use the area formula for the same .

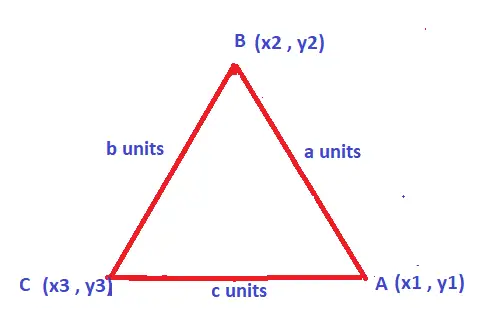
Let say we have three vertices as A (x1 , y1)  ,  B (x2 , y2) and C (x3 , y3)  , Now we have the area of triangle formula as :

Area of Triangle :  (1/2) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]   sq units 

Now here we can even apply the Heron’s formula , by finding the length of each side separately using the distance formula and then applying the Heron’s formula .

Now if you see that one of the vertex is origin above , then the calculation will get simpler and also we have area formula in that case too :

Area of triangle if one vertex is Origin :  (x2*y3  –  x3*y2)/ 2

Where , we have considered the vertex A as origin and computed the above formula . If you want you can manually put values of point A(x1 , y1)  as (0,0) 

Hope you really liked this post regarding the methods to find the area of triangle . Let me know if you have any doubts regarding this topic . Stay tuned for more interesting stuff in this series .