How To Find Domain And Range Of A Function – Detailed Guide (With Shortcuts !!)

Domain and range of a function are indeed one of the most important topics in mathematics that eventually help you to solve any question in algebra (including Graphs) or Trigonometry etc . With the concept of domain and range of any function, you can quickly find out the min and max value that any function can achieve precisely.

In this post we’ll explore all the different types of methods we can use to find domain and range of a function easily . So just relax and read on further .

So firstly we will start with the basics and then gradually we’ll move further into each type of function step by step (with different ways of solving them) . Also later we’ll see some shortcut tricks to solve any domain and range problem just within a few seconds .

It’s time to dive into the main coverage points of this post for your ready reference :

• What is domain and Range of a function ?
• How to find domain of a function ? 
• How to find range of a function ?
• How to find domain and range of a function ?
• How to find domain and range of a composite function ?
• Shortcut Tricks to find domain and range
• Solved examples of domain and range 

I really hope that all the topics have been covered here . Don’t worry if something is missed in the above list, because we’ll cover many subtopics in each of the above-mentioned parent topics .

Note : Before we dig deep into this topic , it’s important to know (recap) about the brackets used for marking intervals on the number line . Always remember that while finding domain and range ,we’ll mainly use two types of brackets :

1. Round brackets (also called parathesis) – To represent the values without including the endpoint (point on the x-axis in open inerval) .

2. Square Brackets – To represent the values including the endpoint (a point on the x-axis in the closed interval)

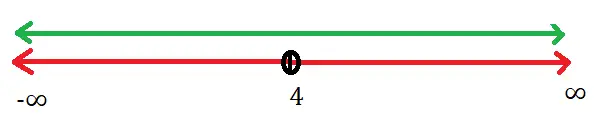
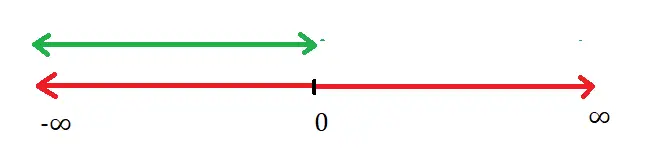
For eg : if the range is given by Range of f(x) = [2,5)  ⇔ This means that the range of the f(x) is all the values in the interval between 2 to 5 , also including the value (point) ‘2’  and excluding the point ‘5’ on the number line as shown below :

Tip : The extreme values in the x-axis i.e. the points ‘infinity‘ and ‘-infinity‘ will never be attached with the square brackets i.e. the infinite point ‘∞‘  should never be associated with the square brackets whatsoever.

Without wasting any further time, let’s start this interesting (bit lengthy :-p) post right away .

What Is Domain And Range Of A Function In Simple Words ?

Let’s understand this in layman terms. For this just consider a candy machine , wherein if you put any amount of coins then you will get an equivalent number of candies from the machine . The concept is simple right .

Now let’s get back to our main topic . Here in mathematics we mainly deal with various kinds of algebraic expressions (i.e. functions and relations) . Hence an algebraic function is specifically defined for a certain range of values and when we put those values in the maths expression, we get the value of the function .

For time being let’s consider a simple function as :

f(x) = x  ;

The above expression is pretty straight forward (isn’t it !) . Now here we can say that for the function f(x),  domain can be defined as all the possible values of “x” in the function (for which function f(x) is defined).

Whereas Range can be defined as all the possible values of f(x) that we obtain after putting different values of x .

Let’ try to correlate this with the candy machine we saw earlier. In that scenario , we can easily say that the coins that we put inside the machine will be the ‘Domain‘  (i.e. different values of x), the number of candies we receive will be the ‘Range‘ (i.e. value of f(x) on putting different values of x) . And the candy machine will act as a mathematical function f(x) indeed .

To memorize this fast , you may remember the above concept as follows :

Domain of a function ⇒ Input Value  (all possible input values)

Range of a function ⇒ Output Value (all possible output values)

To illustrate this theory further, let’s understand one more simple example :

Consider a function given by :

f(x)  = 1/x   ;  (read the function as 1 divided by x)

Clearly, the above function is defined for all real values of x in the number line but not for the one value at which f(x) will become undefined i.e. it will have ‘0’ in the denominator  . Hence the domain for this function is given by the expression

Domain of f(x) = R – {0} ,   (this states that the domain is all real numbers except ‘0’ which makes the function undefined)

Now, clearly on putting (domain values excluding ‘0’) any real value in f(x), we’ll get the range of f(x) as real values in the number line . Hence the range will be all set of real numbers ‘R‘  i.e. (-∞ , ∞)  in the number line satisfying f(x).

Hopefully, now the concept is clear to you i.e. the exact meaning of domain and range of a function . It’s time to understand these two topics in more detail now.

Note : For simplicity , you may find the below notations helpful for your reference (as you will find the below symbols throughout this guide) :

‘∈’ —>  This represents ‘element of’ of ‘belongs to‘ (eg: x ∈ N means x belongs to all natural numbers )

R —>  All Real numbers on the number line

‘ : ‘ — > Read this as ‘such that‘ (eg , x : x – 6 = 5 , read this as x such that x – 6 = 5)

a/b  —>  Read this as a divided by b

a^b —-> Read this as ‘a’ raised to the power ‘b’ (eg , a^2 is simply square of ‘a’)

How To Find Domain Of A Function ?

Frankly speaking , the method to find the domain of a function is much simpler than finding its range . Furthermore, you can easily find the domain by just a mere inspection of the mathematical expression. So always remember the main definition of the domain of a function f(x) :

A domain is the set of values for which the function is defined precisely . 

In mathematical terms, we can say that the domain of a function can be defined as :

Let f : A –> B be a function such that the set A consists of a finite number of elements. Then f(x)  can be described by listing the values which it attains at different points of its domain.  Then set A is known as the domain of f  .

let A = {-2 , -1 , 0 , 1 , 2} and B = {0 , 1 , 2 , 3 , 4 , 5 , 6}

now consider a function f(x) defined as f(x) = x^2      (read it as square of x)

Now if we put different values from set A i.e. {-2,-1,0,1,2} in the above function , we’ll get :

f(-2) = (-2)^2 = 4      ;

f(-1) = (-1)^2 = 1        ;

f(0) = 0^2 = 0        ;

f(1) = 1^2 = 1          ;

f(2) = 2^2 = 4         ;

Clearly each element of set A is associated to a unique element of B . So here we can say that in f : A –> B given by f(x) = x^2 is a function , the domain is given by :

domain (f)  = A = {-2 , -1 , 0 , 1 , 2}     and       range (f) = {0,1,4}  

Note : Two functions f and g is said to be equal if and only if :

domain of f = domain of g

f(x) = g(x) for every x belonging to their common domain

Now let us see the actual methods of finding the domain quickly .

If you want , then you can even find the domain and range of a graph quickly . Just checkout the post here .

How To Find Domain Of A Function Algebraically ?

For simple algebraic equations, you can easily comment on the domain of the function on the basis of the below two conditions i.e. for any function  f(x) , first look for the below conditions right away :

• The denominator of a function should never be ‘0’ (else it will become undefined)
• Inside a square root, a negative value is not allowed

Except for these two conditions, the domain of any function should accept all real values of the number line i.e. ‘R‘ (this conditions mostly holds for majority cases, also in some other cases like logarithms there are some other conditions you may need to check)

So just remember the above two conditions, let’s explore some important varieties of any mathematical function .

How To Find The Domain Of A Function With A Square Root ?

As seen above, here we’ll see the application of the above two rules for finding a domain with square root function .

Let the function given by :

1. f(x)    =    ;

Clearly f(x) assumes real values , if we have the quantity inside the square root as positive value i.e.

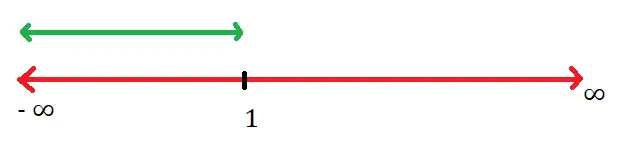
x – 2 ≥ 0 ⇒   x ≥ 2  ⇒ x ∈ [ 2 , ∞ )

Hence the domain of this given function is given by Domain (f) = [ 2 , ∞ ) 

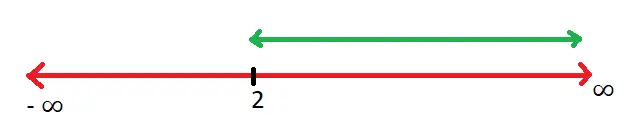
Notice that the value ‘2’ is included and ‘∞’ has been excluded from the domain above.

2. f(x)   =   

 

Now here we have to apply both the rules . We have to ensure the value of x such that the denominator will not become 0 and inside square root we should have a positive value.

Clearly f(x) assumes real value and it is defined for values of x such that :

1 – x ≥ 0  ⇒ x ≤ 1 ⇒  x ∈ (-∞ , 1 ] , but to ensure the first condition i.e. denominator non zero ,

f(x) is not defined at x = 1 . Hence the final domain for f(x) is Domain f(x) = (-∞ , 1 ) in the number line .

How To Find The Domain Of A Rational Function ?

Firstly , what is a Rational function ? . A rational function in maths basically represents a fraction form i.e. p/q form (read p divided by q form) . So a function consisting of both numerator and denominator is said to be a rational function .

So any function of the form of an algebraic fraction for example :

f(x) = 2x + 3y =5  (here dinominator is ‘1’)

f(x) = (4x^3 + 2x^2 + 5x + 8) / (2x^3 + 2x + 7)  is also a rational function containing numerator and dinominator both . (read the symbol ‘^’ as raised to the power)

In practice we will mainly deal with the Real valued function . Now what is this this real valued functions ?

A function f : A –> B is called a real-valued function, if B is a subset of R(set of all real numbers) . If Aand B both are subsets of R , then function f is called a Real function .

Normally a real function is desired by giving some maths expression or formula describing it without specifying the exact domain .

For eg if f(x) = 3x^4 – 5x^2 +9 , then if we want the value of f(x-1) ,           …..(read the ‘a^b’ as ‘a’ raised to ‘b’)

then we must simply put the value of ‘x’ as ‘x-1’ i.e.

f(x-1) = 3(x-1)^4 – 5(x-1)^2 + 9 = 3x^4 – 12x^3 + 13x^2 – 2x + 7                     …….   (on solving)

Here for sake of simplicity and ease of solving we will mainly concentrate on the following forms of a rational function forms :

f(x) =  quadratic/linear ;      f(x) = linear/linear ;    f(x) = linear/quadratic ;        f(x) = quadratic/quadratic   ;

A quadratic equation is of the form : ax^2 + bx + c = 0 (degree of the quadratic equ should be 2 and for  linear equation the degree is 1)

How To Solve For Domain In The Rational Function Of The Form ( linear/linear  ) ?

Now let us consider the function given by :

f(x)     =      linear / linear    =     (x-1)/(x-3)

Again use the same two rules given above for finding domain , (here also check for the ‘x’ value for which the denominator is becoming ‘0’ )

Clearly for x = 3 , the function is undefined , thus the domain of this real function f(x) is given as :

Domain of f = R – {3}  (i.e. all real values except the value ‘3’)

How To Solve For Domain In The Rational Function Of The Form ( Quadratic/linear  ) ?

Now let us consider the function given by :

f(x) = Quadratic / linear = (x^2 – 5x + 4) / (x – 3)

Again use the same two rules given above for finding domain , (here also check fo the ‘x’ value for which the denominator is becoming ‘0’ )

Clearly for x = 3 , the function is undefined , thus the domain of this real function f(x) is given as :

Domain of f = R – {3}  (i.e. all real values except the value ‘3’)

How To Solve For Domain In The Rational Function Of The Form (Quadratic/Quadratic) ?

Now let us consider the function given by :

f(x) = Quadratic / Quadratic =  (x^2 + 3x + 5) / (x^2 – 3x + 2)                 …..(read the ‘a^b’ as ‘a’ raised to ‘b’)

Again use the same two rules given above for finding domain , (here also check fo the ‘x’ value for which the denominator is becoming ‘0’ )

Clearly for x = 1 and x= 2 (On finding the roots of the quadratic equation present in the denominator) , the function is undefined , thus the domain of this real function f(x) is given as :

Domain of f = R – {1,2}  (i.e. all real values except the value ‘1’ and ‘2’)

How To Solve For Domain In The Rational Function Of The Form ( Linear/Quadratic  ) ?

Now let us consider the function given by :

f(x) = Linear / Quadratic =   (3x + 5) / (x^2 – 5x + 4)                      …..  (read the ‘a^b’ as ‘a’ raised to ‘b’)

Again use the same two rules given above for finding domain , (here also check fo the ‘x’ value for which the denominator is becoming ‘0’ )

Clearly for x = 1 and x= 4    (On finding the roots of the quadratic equation present in the denominator) , the function is undefined , thus the domain of this real function f(x) is given as :

Domain of f = R – {1,4}  (i.e. all real values except the value ‘1’ and ‘2’)

Finally we’ve covered all the types of rational function for finding the domain values . Now we’ll see some special type of functions where you can directly comment about the domain straight away :

1. For a constant function i.e. f(x) = k (const) for all x ∈ R , domain is simply the whole real values in the number line i.e. R .

2. For a modulus function f(x) = |x| , the domain is simply the range of all real values i.e.R.

3. For a Greatest integer function (GIF) , f(x) = [x] , the domain is simply the range of all real values i.e.R.

eg of GIF , [2.85] = 2 , [-7.45] = -8 , [6.93] = 6 (this function is also called step function)

4. For a logarithmic function i.e. f(x) =

  for x > 0 , now the domain of this log function is set of all non negative real numbers i.e. (0,∞) .

Also remember that the value of ‘a‘ in the above log function is always a positive value and it should be not equal to ‘1’ .  (a> 0  and a ≠ 1)

5. The domain of the square root function i.e. f(x) =   is all positive values of R i.e. [0,∞) and for the cube root function f(x) =   , the domain can be given as R i.e. (-∞ , ∞) in the number line .

How To Find Range Of A Function ?

Till now we have seen the different ways to find out the domain of any function algebraically. Now its time to explore the steps to find out the range of a function. The other name for ‘Range’ is ‘Images‘. So if we say images of any function f(x) , it simply means the same thing.

Let’s recap the definition of the range of any function :

The range of any real function of a real variable is set of all real values taken by f(x) at points in its domain . Precisely we can say this range as the output values we get on putting different values from the domain of f(x) .

Finding the range of a real function f(x) is somewhat trickier and needs a different approach every time we encounter a maths function . That being said, we need to follow the below given sequence of steps to find the range of any given function explicitly :

1. First put y = f(x)

2. Now solve the equation y = f(x) for ‘x’ in terms of y . Now let x = Φ(y)              … (a different function)

3. Find the values of ‘y’ for which the values of ‘x’ , obtained from x = Φ(y) , are real and in the domain of f .

4. The set of values of y obtained in the previous step is the range of function f .

The above steps might confuse you at your first glance, so it’s indeed imperative to jump to the next section to make the steps ample clear to you . (trust me, it’s really easy)

How To Find Domain And Range Of A Function ?

To make the above steps clear in this section, we’ll look into some easy problems here to make the concept clear . So let’s start digging into the examples straight away and find the domain and range as below:

1. f(x) = (x – 2) / (3 – x)

Clearly domain of f(x) can be evaluated easily by using the two rules given at the start . Here clearly the given function is defined for all values of ‘x’ except 3 , where the denominator will become ‘0’ and f(x) becomes undefined .

Now to find the range , we’ll use the four-step rule mentioned above :

1. f(x) = y

2. y   =   

On solving , x(y + 1) = 3y + 2 ;

Then    x   =     ;

Clearly x assumes real values for all y except y = -1 . Hence range of f = R – {-1}

2. f(x)   =   (x^2 – 9) / (x – 3)

Clearly domain of f(x) can be evaluated easily by using the two rules given at the start . Here clearly the given function is defined for all values of ‘x’ except 3 , where the denominator will become ‘0’ and f(x) becomes undefined .

Domain of f = R – {3}      (all real values except 3 in the number line)

Now to find the range , we’ll use the four-step rule mentioned above :

1. f(x) = y

2.   y    =      =      =   x + 3      (using identity a^2 – b^2 = (a+b)(a-b)  )  ;

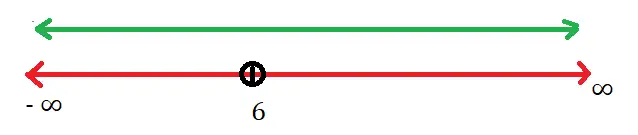
thus finally , y = x + 3 

also we can say    x  =   y – 3                                                          ….. (but y = f(x) not defined at x = 3)

It follows from the above relation that y takes all real values except 6 when x takes values in the set R – {3}  . If y assumes value ‘6’ , then x will result into ‘3’ which makes the f(x) undefined .

Thus the range of f(x) = R – {6}

Note : The four-step rule can sometimes lead to complex calculations and it becomes tough to express f(x) in terms of ‘y’ . At that time you may even use common sense to comment on the range of the function .

Let’s try one by inspection :

f(x)    =     

Clearly the domain of the above function is R as we can put any value of x to get different values of f(x) . In the denominator, we can no way make it 0 (isn’t it !) . Now to find the range , just observe the function carefully :

f(x)    =   

in the numerator and denominator, we have two square terms which always results in the same value for f(x) (when we put any value for ‘x’)

So let’s find out the min value of the expression by putting x = 0 (we put x = 0 as we already know the expression will result in a positive value always)

On putting x = 0 , min value of f(x) = 0 we get .

Now in the numerator and denominator, we can see square terms , which further make us conclude that the max value will never attain ‘1’ .

for eg , put x = 2 , x = 5 , x = 7 etc , always an extra ‘1’ will be added in the denominator which eventually make the f(x) value close to ‘1’ and not exact ‘1’

Thus ,we can conclude that the range of f = [0,1)

In this way, we can find the range by using some different approaches and accomplish our mission of finding a range of f(x) .

Now its time to see some complex rational functions and the way to find its range and domain systematically.

How To Find Domain And Range Of A Rational Function Of The Form (Linear/Quadratic) ?

Consider the below function f(x) , and let’s find out the range and domain :

    f(x)     =   

The domain of the above function is clearly R i.e. (-∞ , ∞)  in the number line . (in other words there is no value where the function will become undefined)

Now its time to find the range of f(x) by the four-step rule mentioned above :

1. Let y = f(x)

2. Now we have to express f(x) in terms of y

y   = 

Then ,       y + yx^2 = x ;

Also  ,      yx^2  – x + y = 0

Now this is a quadratic equation of the form   :  ax^2 + bx + c = 0

where a = y , b = -1 , c= y

Now we know the roof of any quadratic equ is given by

x   = 

Putting the values of a, b ,c above , we get :

x     =          …(D ≥ 0 for real roots)

On solving the above equations , we will get the two roots . But we are interested in the domain where the value of ‘x’ is possible . So our main concentration should be inside the square root , which should be a positive term . (also the denominator should not be zero i.e. y ≠ 0  )

Then ,     1 – 4y^2 ≥ 0 ;

  On solving ,

(y – 1/2)(y + 1/2)  ≤ 0             …….  (we know Inequality sign changes on multiplying with ‘-‘ sign throughout the equ)

now lets plot this on the number line as below :

y ∈  [-1/2 , 1/2]  (we’ve used square brackets as we have an inequality with the ‘equal’sign) and also y ≠ 0 (as the denominator should not be zero)

Now we get the range of values for which ‘x’ is defined , now let’s compare this values with the actual equation of y = f(x) , So as per this , f(x) will never become ‘0’ on any value of ‘x’  so if we put x = 0  then value of f(x) is becoming ‘0’

f(x)     =       ;

f(0) = 0 / (0+1) = 0    ;   

This simple states that the condition y ≠ 0 is not valid (condition) and should not be included as the range of f(x) (because we are getting range of f(x) as ‘o’ for the value  x = o ) .

Thus the final result is that the domain of f is R and range of f = y ∈  [-1/2 , 1/2] 

How To Obtain Domain And Range Of A Quadratic Function ? (Function Of The Form Quadratic/Quadratic )

There are a total of three formats of rational function possible that includes a quadratic polynomial in the algebraic function i.e.

f(x) = (quadratic/linear) or (linear/quadratic) or (quadratic/quadratic)

Apart from the last format , all other formats are already seen in the previous sections .

To obtain domain and range of quadratic equations , it is a little complex and needs a regular practice indeed . Also here there is one additional step you should follow along with the four-step process mentioned above for finding the range .

For finding the domain and range of quadratic equations , we have to follow the below five steps (first four is same and the last one is the additional step added in this) :

1. First put y = f(x)

2. Now solve the equation y = f(x) for ‘x’ in terms of y . Now let x = Φ(y)              … (a different function)

3. Find the values of ‘y’ for which the values of ‘x’ , obtained from x = Φ(y) , are real and in the domain of f .

4. The set of values of y obtained in the previous step is the range of function f .

5. Lastly do check for the value of ‘x’ (if any) for which y will become ‘0’ . Then finally conclude the range and domain values. We need to equate the coefficient of the x^2 in equ we get in step 3 above.

This will be clear once we start solving the problems. Let’s find the domain and range of the function given as :

f(x)  =   3 / (2 – x^2)

Clearly domain of this function is R – {√2 , -√2} , at these points the f(x) will become undefined (as the denominator will become 0).

Now its time to find the range, again let’s follow the five-step process mentioned above :

y = f(x)    =      ;

On solving  (we want a quadratic equ in terms of y),

Then  ,    2y – xy^2 = 3 ;

Also ,     yx^2 – 2y + 3 = 0 ;

This is a quadratic equ ,where we have the coefficients as :

a = y , b = 0 , c = -2y+3

Now we know that for real roots of any quadratic equation , the discriminant should be greater than equal to 0 i.e.

Hence  ,   b^2 – 4ac ≥ 0

Now put the values ,

i.e.      0 – 4y(-2y+3) ≥ 0  ;

On solving , we get 8y^2 – 12y  ≥ 0   ;

i.e.      (y)(2y – 3) ≥ 0

The range of values for y supporting the above inequality should be :

i.e.       Range = (-∞,0] U [3/2 , ∞)

Now the most important last additional step we need to follow here  :

Put y = f(x) = 0

3 / (2 – x^2)  = 0 ;

On solving we get 0 = 3 which is invalid i.e. there is no value of ‘x’ for which f(x) will become ‘0’ . Thus we can’t include the point ‘0’ as range of f(x)

Finally the range of f(x) will be (-∞,0) ∪ [3/2 , ∞)

Notice that the point ‘0’ has been excluded by using square brackets above .

Now let’s look into the last format that is quadratic/quadratic function : 

f(x)     =     ;

So lets find out the domain and range of the above quadratic equation using the mentioned five step process .

So lets y = f(x) = 

Then ,         yx^2 + yx+ y =  x^2 + x + 2                                …..  (read the ‘a^b’ as ‘a’ raised to ‘b’)

On solving ,

(y-1)x^2 + x(y-1) + (y-2) = 0

Now this is a quadratic equation , coefficients will be :

a = y-1 , b = y-1  , c = y-2

For quadratic equ having real roots (since is defined for only real roots) , we know the condition as :

b^2 – 4ac ≥ 0                               …… (discriminant should be greater than equal to ‘0’ for real roots)

Now putting the values , of the coefficients

(y-1)^2 – 4 (y-1)(y-2) ≥ 0                            …..  (read the ‘a^b’ as ‘a’ raised to ‘b’)

On solving the above equation ,

3y^2 – 10y + 7 ≤ 0                            …..(sign of inequality changes on multiplying with ‘–‘ throughout the equ)

Thus , (3y – 7)(y – 1) ≤ 0

Lets plot this on number line and get the values satisfying the above condition (inequality)

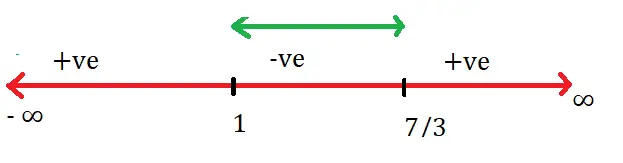
Hence value of y ∈ [1, 7/3]       ………. (both the endpoints included)

Now in step 3 above , we got the quadratic equ as

(y-1)x^2 + x(y-1) + (y-2) = 0

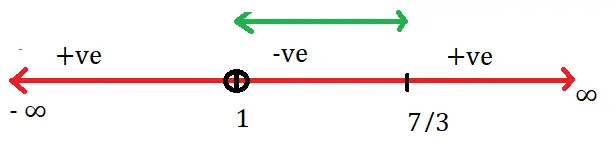
Now lets equate the coefficient of x^2  as 0 i.e.    y-1 = 0 ‘

Thus y = 1 = f(x) 

1 =   

On solving the above equ , we can check whether there is any value of x for which we get the value of f(x) as 1

Then , x^2 + x + 2 = x^2 + x + 1                             …..  (read the ‘a^b’ as ‘a’ raised to ‘b’)

2 = 1 ; which is false

thus there is no value of ‘x’ for which we’ll get the value of f(x) as ‘1’

Hence we should not include the point ‘1’ in the range of f(x) .

Finally, the range of f(x) can be given by : Range of f =  (1, 7/3]          …. (the point ‘1’has been excluded by using the round brackets )

How To Find Domain And Range Of A Composite Function ?

What do we mean by composite functions ? So a composite function basically consists of more than one function being operated upon by various mathematical operations (like a simple add , subtract , product or division) . Till now we have seen the method to find the domain and range of a single function at a time .

Now here we’ll deal with say two separate functions f(x) and g(x) with different domains and range values . Firstly we will see a simple problem containing function of functions , then eventually we’ll proceed further with the different operations based on functions .

Consider two functions as f(x) = 3x – 12 and g(x) = √x , Now find the domain and range for the following functions as given below :

1. f(g(x))     And    2. g(f(x))

1. First we need to find the domain and range of f(g(x))

This simply means that we need to put the value of the function g(x) in the place of ‘x’ and find the final function f(x) as shown below :

Since g(x) = √x ,

Now f(g(x))  =   f(√x)  =  3√x  – 12  —->  This is our final function ,that we need to evaluate for domain and range .

Clearly domain of the function f(g(x)) =  3√x  – 12 is  all positive R values including ‘0’ i.e. [0,∞)

Hence the domain of f(g(x)) is  { x ≥ 0 | x ∈ R }

Now range can be calculated as just by inspection i.e. for the minimum value of x in it’s domain , f(g(x)) gives value as ‘-12’ ( since the min value that x can take is ‘0’ , by putting this in the function we get min value of the range as ‘-12’)

And the max value it can take is ‘∞’ , so the max value of the function f(g(x))  will be ‘∞’  .  (since it is a polynomial function)

Range of the function f(g(x))  is { y ≥ -12 | y ∈ R }                  ……. where y = f(g(x))

2. First, we need to find the domain and range of g(f(x))

This simply means that we need to put the value of the function f(x) in the place of ‘x’ and find the final function g(x) as shown below :

Since f(x) = 3x – 12 ,

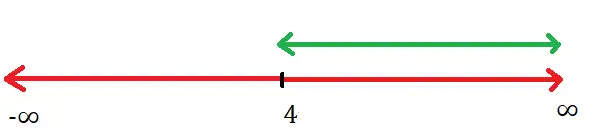
Now  g(f(x))  =   g(3x-12)  =  √(3x-12)  —->  This is our final function ,that we need to evaluate for domain and range .

Clearly domain of the function g(f(x)) = √(3x-12)   is  :

3x – 12 ≥ 0 ;        (anything inside root should be positive)

Thus ,  the domain will be x ≥ 4  or  x ∈ [4 , ∞)

Hence the domain of g(f(x)) is  { x ≥ 4 | x ∈ R }

Now range can be calculated as just by inspection i.e. for the minimum value of x in it’s domain , g(f(x)) gives value as ‘0’ ( since the min value that x can take is ‘4’ , by putting this in the function we get min value of the range as ‘0’)

And the max value it can take is ‘∞’ , so the max value of the function g(f(x))  will be ‘∞’  .  (since it is a polynomial function)

Range of the function g(f(x))  is { y ≥ 0 | y ∈ R }                  ……. where y = g(f(x))

Note : The sum , difference , product, and quotient are defined for real functions only on their common domain . Thus for example , if we have the addition operation to be performed , we can say that :

Let f : D1 –> R and g : D2 –> R be two real functions . Then their sum f + g is defined as that function from D1 ∩ D2 to R which associates each x ∈ D1 ∩ D2 to the number f(x) + g(x)

Here D1 and D2 are the domains of the function f(x) and g(x) respectively . Thus we can say that :

(f+g)(x) = f(x) + g(x) for all x ∈ D1 ∩ D2 ;

Likewise for subtract, product, quotient  operation, we can define in a similar manner :

(f * g) (x) = f(x) g(x)  for all x ∈ D1 ∩ D2  ;

(f – g) (x) = f(x) – g(x) for all x ∈ D1 ∩ D2  ;

(f/g) (x) = f(x) / g(x)  for all x ∈ D1 ∩ D2  – {x : g(x) =0}

On multiplication of a function by a scalar (real number say ‘α’) :

(αf)(x) = α f(x)  for all x ∈ D

Now lets try out a simple problem based on this composite real functions to make this concept clear :

Let f and g be two real functions defined by :

f(x) = 1/(x+4)    and    g(x) = (x+4)^3

Find the following :

1. f + g            2. f – g              3. f*g             4. f/g              5. 1/f            6. 1/g          7. 2f

Firstly we need to find their common domain (operation on real functions is defined only on their common domain as stated earlier)

Clearly for the function  f(x)  =  1/(x+4)  , this is defined for values of x except x = -4 (at which denominator will become ‘0’)

Domain of f = R – {-4}      (all real values except ‘-4’ )

Now for the next function g(x) = (x+4)^3      , clearly this is defined for all values of ‘x’ which make us to conclude its domain as : Domain of g = R  ( i.e. g(x) is defined for all values of x ∈ R)

Now their common domain D1 ∩ D2 is given by Domain of (f) ∩ Domain of (g) = R – {-4}

1. (f+g)(x) = f(x) + g(x) for all x ∈ D1 ∩ D2

(f+g)(x)   =   1/(x+4)  +  (x+4)^3    = 

2. (f-g)(x) = f(x) – g(x) for all x ∈ D1 ∩ D2

(f-g)(x)   =   1/(x+4)  –  (x+4)^3    = 

3. (f.g) (x) = f(x) g(x)  for all x ∈ D1 ∩ D2  ;

(f.g)(x) = f(x) . g(x)  =  (x+4)^2

4. (f/g) (x) = f(x) / g(x)  for all x ∈ D1 ∩ D2  – {x : g(x) =0}

f(x)/g(x)  =  1/ (x+4)^4    for all x ∈ R – {-4}

5. (1/f)(x) = 1/(f(x)) = x+4

6. (1/g)(x) = 1/(g(x)) =  1/(x+4)^3  for all x ∈ R – {-4}

7. (2f)(x) = 2 (f(x)) = 2/(x+4)  for all x ∈ R – {-4}

In the next section we’ll further see some useful tricks to solve the domain and range problems of certain type quickly . So let’s proceed further .

Shortcut Tricks To Find Domain And Range Of A Function   !!

The methods we’ll discuss here are not exactly shortcuts , these are some proven techniques that you may use to get the results fast  (consider these as just some time-saving methods).

Firstly let us see the domain and range of basic trigonometric functions (keep them handy always) :

Trigonometric Function	Domain	Range
Sine Function (sinθ)	θ  ∈  R	[-1,1]
Cosine Function (cosθ)	θ  ∈  R	[-1,1]
Tangent Function (tanθ)	θ  ∈  R  – {(2n+1) x 90°}	[-∞,∞]

Now with this knowledge, we can directly use this to predict the domain and range of any function including the trigonometric functions. Let’s see some applications :

It is very much evident from the above that the domain is always ‘R’  for these trigonometric functions , so we’ll mainly concentrate on finding the range .

Shortcut tip 1 :

If the function is given in the form  :

f(x)  =   

in place of  sinθ and cosecθ , we can also have any other reciprocal combinations like (tanθ , cotθ) and (cosθ , secθ)

So two conditions before you use this shortcut :

1. Both the trigonometric function should have the same angle

2. The trigonometric function should include a reciprocal pair and both should be in the square form

3. There should be a ‘+’  in between both the terms (addition)

If these three conditions satisfied, then we can directly say that the min and max value of the range as :

Min value of f(x) = 2√(ab)      and      max value of f(x) = always infinity (∞)

This will be clear on solving the below examples.

Find the range (min and max values) for the below functions :

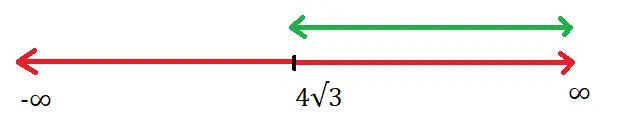
1. f(θ)   =   

Clearly the angle is the same in both the trigonometric terms i.e. theta and also both the terms are reciprocal of each other (sin and cosec)  and also a ‘+’ sign in between.

Applying the formula :

Min value of the range : 2√(ab)  =  2√(3*4)   =   2√12  =  4√3

Max value is infinity

The range is given as :   Range of  f(θ) = [4√3 , ∞)

2  f(x)  = 

Clearly the angle is the same in both the trigonometric terms i.e. 2x  and also both the terms are reciprocal of each other (cos and sec)  and also a ‘+‘ sign in between .

Applying the formula :

Min value of the range :   2√(ab)  =  2√(9*16)   =   2√144  =  24

Max value is infinity

The range is given as :   Range of  f(x) = [24 , ∞)

Shortcut tip 2 :

This method will only include sine and cosine terms , lets see if a function given in the form as :

f(x) = asinx + bcosx        …….. (a , b can be a positive or negative integer i.e. their sign doesn’t matter)

then the min and max value of the range will vary from

Min value = -√(a^2 + b^2)              Max value =  √(a^2 + b^2)

Range can be given as =  [-√(a^2 + b^2)  ,  √(a^2 + b^2)]                 ….. (in closed interval)

Conditions to be checked for this method :

1. For both the sine and cosine terms , angle should be the same

2. There should not be any different domains given for each sine and cosine terms . (there should not be any different domain for each)

Note : Here , in the function, if we have different signs of ‘a’ and ‘b’ , then also the formula is valid as we have square terms in the formula.

Find the range for the function :

1. 3sin4x – 4cos4x

Clearly the angle is same,  and no specific domain mentioned. So we’ll directly use the above method .

here a = 3 and b = -4

Min value is = -√(a^2 + b^2) = -√(3^2 + (-4)^2)  = -5    ;

Max value of f(x) = √(a^2 + b^2) =  √(3^2 + 4^2) = 5     ;

Range of f(x) =  [-5,5]

2.    -4cos5x – 3sin5x  – 5

Here we have the function as :  f(x)  =  -4cos5x – 3sin5x  – 5

let assume ,     g(x)  = -4cos5x – 3sin5x   , such that f(x)  =  g(x)  – 5

Min value of g(x) =  -√(a^2 + b^2)  =   -√(3^2 + 4^2)   =    -5

Max value of f(x) = √(a^2 + b^2) =  √(3^2 + 4^2) = 5

Range of g(x)  =  [-5,5]

Now we have f(x) = g(x) – 5

Range of f(x)  =  [-5  – 5 ,5 –  5]   =   [-10 , 0]

3. Shortcut tip 3 :

We already know the range of basic trigonometric functions i.e. sine , cosine, and tangent functions . So we can easily apply this logic in solving other functions involving these trigonometric functions .

Find the range for the function :

f(x) =  4sinx + 6         

Now here we have a function including a trigonometric function sinx , as we already know that the range of a sine function varies in between  -1 to 1 i.e. 

     Range of sinx =      -1   ≤ sinx  ≤   1   ;

But we want the range for the function i.e.   4sinx + 6 , for this we need to transform the above inequality condition satisfying the given function :

We have :    – 1   ≤ sinx  ≤   1     ;

Now multiplying with 4 throughout this equation , 

i.e.       – 4   ≤  4sinx  ≤   4                …….( no affect on the inequality sign-on multiplying with a constant value )  

Now , adding ‘6’ through the equation :

 i.e.      – 4  +  6   ≤  4sinx  + 6   ≤   4 + 6   

This implies :    2   ≤ 4sinx  + 6 ≤   10

Finally we get the range of the f(x)   as     [2,10]

Similarly, we can evaluate functions involving cosine and tangent functions.  

How To Find Domain And Range Of A Function Using AM and GM Method ?

With AM ad GM we basically mean the Arithmatic mean and Geometric mean  respectively . Till now we have been using the traditional ways of finding the domain and range of any function .

However, with AM and GM , we can quickly find the min/max value of functions . 

Let’s understand what is AM and GM first , let a and b be two positive integers , then 

AM = (a + b) /2     and       GM  =  √(ab)

And , always the condition holds true i.e. AM ≥ GM

Also if we have three integers then , 

AM = (a + b + c) /3     and       GM  =  (abc)^ (1/3)                                  …..(read the ‘a^b’ as ‘a’ raised to ‘b’)

So AM and GM valid for any number of positive integers , So the main condition before applying this logic is to check whether the numbers are positive or not .

Also we need to check for equality to find the value of ‘x’ at which the two functions will be equal . If there is no value then we can’t apply this logic . 

Note: Both the functions should be a reciprocal of each other so that they can cancel each other and give a constant value inside the root . 

Let’s find the range for the function f(x)  = 

So now how to inspect that whether we can apply the AM and GM logic here or not ?

here we have two parts in the function f(x)  i.e.    a = x^2     and   b = 4/(x^2)

Also, both part is positive. And both parts are reciprocal of each other (ignore the constant ‘4’ for time being)

Thus we can apply the AM and GM method  here as below :

    AM ≥ GM        ⇒        (a + b) /2    ≥    √(ab) 

Hence we can write  :        (a + b)    ≥    2√(ab) 

Now putting the values of a and b above , we get 

           ≥      2 √ [x^2  *   (4/x^2)]

Thus ,         ≥    2 * 2 

or              ≥    4

Now we can saythat the function f(x) may have minimum value of ‘4’ , for confirming this we need to check for the equality point of ‘x’ 

let’s equate a and b now , i.e.    a  =  b

       x^2   =    4/x^2    ,                                                            …..(read the ‘a^b’ as ‘a’ raised to ‘b’)

 Now,    x^4   =  4 

On solving we get ,    x  =  ±√2 , so a value exists for these two function at which they are equal . Thus now we can say that the value  ‘4’ is the minimum value of the range of f(x) 

Now for max value , let put x = ∞ ,   

then we get f(x)  =  ∞   +   4/∞    =  ∞    

Sothe max value of f(x) is infinity . Finally we can say that the range of f(x) is  [4,∞)   

Likewise in place of ‘x’ , we may have trigonometric functions that are reciprocal of each other like the pair (sine,cosec) or (cosine,sec) etc , then we can simply use this AM and GM trick to find out the range of f(x)

Miscellaneous Solved Examples Of Domain And Range Of A Function !!

Till now we have seen many examples of different types . Let’s take this legacy forward and try some different types of functions to give you a glimpse of different approaches to find domain and range . 

Let’s find the domain of the function :

f(x)    =       ;

Here we have an inverse trigonometric function , and we now that   is defined for all the values of ‘x’ ranging from [-1,1]

that means ,        -1  ≤  x  ≤   1   

but here we have , x^2 – 3 in place of ‘x’ , that means  :

-1  ≤  x^2 – 3  ≤   1   , now we have two functions here as follows :

x^2 – 3 ≥ -1          and      x^2 – 3 ≤ -1  

Now we need to find the common values of ‘x’  satisfying both the functions . 

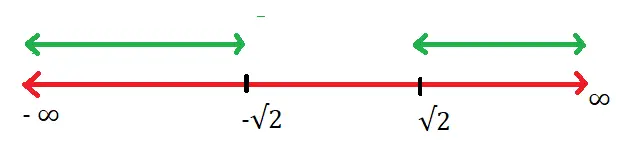
f1(x)    =  x^2 – 3 ≥ -1      ;

i.e.       x^2 – 2  ≥   0    or   (x + √2)(x – √2) ≥   0

Domain is =   (-∞ , -√2] ∪ [√2 , ∞ )

f2(x)    =  x^2 – 3 ≤ -1       ;

on solving ,    (x + 2)(x – 2)  ≤  0  

Domain is = [-2,2]

Now we need to find the common domain (values of x satisfying both equ) for both these equations , on solving we get the common values of ‘x’ as follows :

Domain of f1(x)  ∩  Domain of f2(x)  =   [-2 , -√2] ∪ [√2 , 2]

2. Find the domain for the function :

f(x)  =    

Here we have a modulus function and also a square root function in the denominator . So clearly this function is defined for all x except for the value at which the denominator will become ‘0’ . 

So now to find the domain we can say that the below condition should be satisfied as :

|x| – x > 0           …. (equal to sign is not valid as the f(x) will become undefined)

Now we have  ,    |x|  > x

Now let x= 0   , we have 

0 > 0   which is not possible 

Now put x = 1  , 

Then  1  >  1   , which is not possible  

Now finally put  x = -1  ,

Then   1  > -1   which is correct

Finally, we can conclude that the domain of f(x) is defined only for the negative values of ‘x’ . 

Domain of f(x)  =  (-∞ ,  0)

Do let me know if you want more examples on this topic  . The practice is the key here .If you have any doubts , let me know in the comments section . 

Last but not the least, we can easily solve the domain and range problems using the graphical methods . Stay tuned for more interesting stuff in this series .