How To Find The Vertex Of A Parabola In Equation Using Vertex Form And Standard Form!! [With Steps & Examples]

A parabola forms an integral part of the conic section geometry( among others like ellipse, hyperbola etc). There are many important terms related to parabola, that we frequently come across i.e. the focus, directrix, Axis, vertex etc . In this post we will explore all the different variety of methods that can be used to find the vertex of parabola. We already know that there are a total of four types of parabola i.e. a vertical or horizontal parabola depending upon the equation of a parabola.

Here we’ll explore the different types of parabola with solved examples. We’ll study the vertical type of parabola (the upward and downward opening parabola) and the horizontal parabola (opening sideways ). Also, we will learn about the standard parabola equation and the vertex form of parabola equation.

Without wasting any further time , let’s get started.

How To Find The Vertex Of A Parabola?

Steps to be followed to find the vertex of a parabola :

• Firstly form/find out the equation of the second-degree parabolic curve (if the equation is given then well and good !!)
• Then check the form of the equation (standard/quadratic/reducible to standard form)
• Apply the steps each for the standard/reducible to standard form and the quadratic equations 
• If nothing is clear from the equation, then try to find the vertex of a parabola using graph of parabola

In order to understand the exact process as mentioned above , you need to go through the descriptive part below . So just relax and read further . (we’ll initially start with the parabola basics, feel free to skip it if you wish to !!)

If you want to find the vertex of parabola using graph , then check this article out . 

What Is A Parabola And It’s Vertex ?

A parabola is the locus of a point which moves in a plane such that its distance from a fixed point in the plane is always equal to its distance from a fixed straight line in the same plane. The fixed point is called the focus (point S) and the fixed straight line is called the directrix (Line ZZ’ below) of the parabola.

The line through the focus and perpendicular to the directrix is the axis of the parabola . And the point on the axis midway between the focus and directrix is called the vertex of the parabola.

The parabola has two real foci situated on its axis one of which is the focus and other lies at infinity. The corresponding directrix is also at infinity.

With the axis of symmetry (x axis above i.e. y = 0), we basically mean that a perpendicular line is drawn through the parabola (vertex) such that for every positive value of ‘x’ there are two equal and opposite values of ‘y’ for the equation y² = 4ax. 

The focus ‘S’ of the parabola y² = 4ax is at (a,0) and the directrix is x = -a . The axis is a line passing through the focus and perpendicular to the directrix i.e. the x-axis or y = 0 , is the axis of the parabola y² = 4ax. The axis meets the curve y² = 4ax at the origin.

So, the coordinates of the vertex is (0,0) . Clearly the vertex is a Midway between the focus and the directrix that is the vertex is always equidistant from the focus and the directrix. So for any parabola, we generally have four standard forms that are :

y² = 4ax     ;     x² = 4ay    ;  y² = -4ax      And      x² = -4ay  ;

Moreover , the Latest rectum (LL’ above) of a parabola is a chord passing through the focus and perpendicular to the axis of the parabola. Finally, a focal chord (line SP above) is any chord passing through the focus of a parabola.

How To Find The Vertex Of A Parabola In Its Standard Form Equation?

This type is the simplest form of all the other types to find the vertex of a parabola. Here , sometimes you don’t even need to touch your pen or paper . Most of the time you can predict the value of the vertex just by a simple glance (isn’t this easy ?) the given parabolic equation .

So for any parabola, we generally have four standard forms that are :

y² = 4ax     ;     x² = 4ay    ;  y² = -4ax      And      x² = -4ay  ;

The shapes of the graph in all the above four forms will be different depending upon the choice of axes . Also for ready reference, we can refer the below table with the values for the important aspects related to any parabola :

Parabola Parameters	y² = 4ax	y² = -4ax	x² = 4ay	x² = -4ay
Coordinates of vertex	(0,0)	(0,0)	(0,0)	(0,0)
Coordinates of focus	(a,0)	(-a,0)	(0,a)	(0,-a)
Equation of directrix	x = -a	x = a	y = -a	y = a
Equation of the axis	y = 0	y = 0	x = 0	x = 0
Length of Latus-rectum	4a	4a	4a	4a
Focal distance of any point P (x,y)	a + x	a – x	a + y	a – y

From the above table , you can easily find the vertex and many other values for any parabola in it’s standard form .

Note : If the vertex of the parabola is at the point A(h,k) and its latus rectum is of length 4a , then its standard form will be :

(y-k)² = 4a(x-h)     ;     (x-h)² = 4a(y-k)    ;  (y-k)² = -4a(x-h)      And      (x-h)² = -4a(x-k)  ;

Basically then we need to shift the x and y axis to new point , to reduce it into the standard form .  Let us see some examples to illustrate the above formulas more clear and easy to understand .

Let’s find the vertex , focus , directrix , axis , latus rectum for the given parabola equation :

1. y²  =  -12x     

The above equation is of the standard form as y² = -4ax , on comparing carefully we can compute the values of all the parameters quickly.

Thus ,       4a = 12  or a = 3 ;

Now using the values given in the above table , the focus is at  (-a,0) i.e.  (-3,0)  and the equ of the directrix is x = a i.e. x = 3 .

Length of latus rectum is 4a = 12  , coordinate of the vertex is (0,0)

2. x²  =  6y   

The above equation is of the form  x²  =  4ay   ,  then 4a= 6  , hence ‘a’ = 3/2

Now using the values given in the above table , the focus is at  (0,a) i.e.  (0,3/2)  and the equ of the directrix is y = -a i.e. y = -3/2 .

Length of latus rectum is 4a = 6  , coordinate of the vertex is (0,0)

How To Find The Vertex Of An Equation Of A Parabola Reducible To One Of The Four Standard Forms ?

Now in this type of problems , we need to reduce the complex equation into one of the standard forms by adding /subtracting appropriate values on the LHS (left-hand side) and RHS (right-hand side) of the given equation respectively .

Once the transformed equation resembles one of the standard forms , then we need to shift the origin (0,0) to a new point (h,k)  to use any of the below equations as below :

(y-k)² = 4a(x-h)     ;     (x-h)² = 4a(y-k)    ;  (y-k)² = -4a(x-h)      And      (x-h)² = -4a(x-k)  ;

once the above equation is present ,then we’ll shift the origin to new points (h,k) as :

X = x – h and Y = y – k , then finally we’ll get the below transformed equations :

Y² = 4aX     ;     X² = 4aY    ;  Y² = -4aX      And      X² = -4aY  ;

Now we can simply use the formulas as given in the above table to derive the values of different fields of a parabola .

Let’s see some examples to illustrate this in a clear manner .

Find the vertex , axis , focus , directrix , latus rectum of the following parabola :

1. y² – 8y – x + 19 = 0 

So here , clearly this is not a straightforward standard form of parabola equation . Now we need to transform this into one of the standard forms to derive the values of the vertex , axis , focus , directrix , latus rectum of this parabola .

Given equation is :    y² – 8y – x + 19 = 0   ;

Then      y² – 8y =  x -19  ;

Also      y² – 8y +  16  =  x -19 + 16  ;                         ….(Adding ’16’ both the sides)

As seen above , we’ve added 16 both the sides . Now the term we need to add depends upon the term already present in the LHS i.e. ‘y² – 8y‘  here . The sole motto of this is to reduce the LHS into an identity i.e. either (a+b)² or (a-b)²

Tip : To find the term needs to be added both sides to make a square term in the LHS , just simply add the term i.e. (half the coefficient of ‘x’ or ‘y’ in the LHS )²

Now ,     (y – 4)²  =  (x – 3)         …… [as we know  y² – 8y +  16   =  a² – 2ab + b² = (a – b)²  =  (y – 4)²   ]

Now the above equation is of the form :

(y-k)² = 4a(x-h)   ;

Now we have to shift the origin to a new point (h,k) from the (0,0) point. Also, we have :

X = x – h and Y = y – k  ;          …..(here we have h = 3  and k = 4)

to find the old points (x,y)  , we simple put the values below as  :

x  =  X + h  and   y  =  Y + k      ;             …….  note this as equation 1

We’ll get the below transformed standard equation of the parabola as given below  :

Y² = X      ,     

On comparing the above standard equation with the standard form  Y² = 4aX

we have ,  4a = 1  ,   thus    a = 1/4    ;

Now the vertex of this standard parabola is at (X = 0, Y = 0)  , thus the vertex of the given parabola with respect to the new axis are  (0,0)

So now since we’ve shifted the new origin to (h,k) i.e. (3,4)  . Thus the vertex of the parabola with respect to the old axes are (3,4)         ………….(by putting values of X and Y in equation 1)

The equation of the parabola with respect to the new axes is Y = 0 , so the equ of the axis with respect to old axes is y = 4  ;                     ……..(by putting the value of  Y in equation 1)

The coordinates of the focus with respect to the new axes are (X = a , Y = 0) i.e.   (X = 1/4 , Y = 0)  . So the coordinates  of the focus with respect to old axes will be (13/4 , 4)      …….  (by putting values of X and Y in equation 1)

Directrix equation with respect to new axes is X = -a i.e.  X = -1/4

The equation of the directrix with respect to the new axis will be x = X + 3 =  -1/4 + 3  =  11/4

Length of latus rectum is a constant i.e. ‘4a’  , since here a = 1/4  , Thus length = 4a = 4*  1/4 =  1 

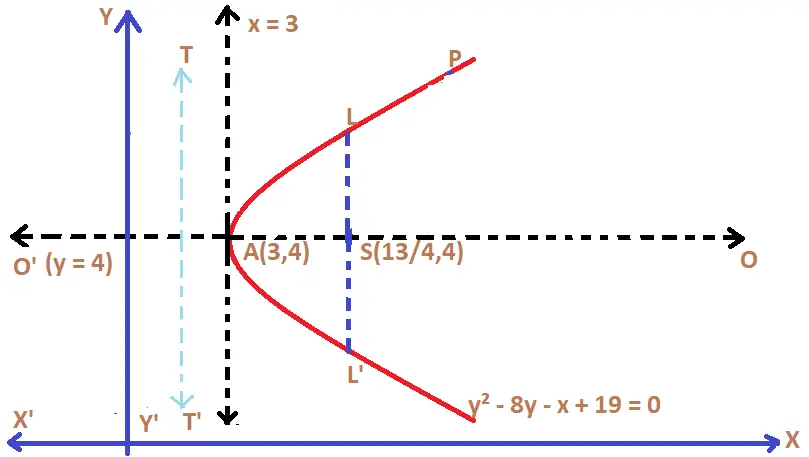
Refer to the above figure , OO’ is the axis of symmetry , point S is the focus, and point A is the vertex of the parabola . XX’ and YY’ are the x and y-axis respectively . LL’ is the latus rectum (length = 1) and TT’ is the directrix at x = 11/4

Hopefully, it is much clear now the shifting of origin concept from the above problem . Basically we mainly use the equation 1 to get the actual result everytime i.e.  x  =  X + h  and   y  =  Y + k  ;

Now let us see one more example :

Find the vertex , axis , focus , directrix , latus rectum of the following parabola :

1. x² + 2y – 3x + 5 = 0 

So here , clearly this is not a straightforward standard form of parabola equation . Now we need to transform this into one of the standard forms to derive the values of the vertex , axis , focus , directrix , latus rectum of this parabola .

Given equation is :  x² + 2y – 3x + 5 = 0

Then      x² – 3x =  – 2y – 5  ;

Also      x² – 3x +  9/4  =  – 2y – 5 + 9/4  ;                         ….(Adding ‘9/4’ both the sides)

As seen above , we’ve added 16 both the sides . Now the term we need to add depends upon the term already present in the LHS i.e. ‘x² – 3x‘  here . The sole motto of this is to reduce the LHS into an identity i.e. either (a+b)² or (a-b)²

Now ,     (x – 3/2)²  =  -2(y + 11/8)         …..[as we know  x² – 3x +  9/4    =  a² – 2ab + b² = (a-b)²  =  (x – 3/2)²   ]

Tip : To find the term needs to be added both sides to make a square term in the LHS , just simply add the term i.e. (half the coefficient of ‘x’ or ‘y’ in the LHS )²

Now the above equation is of the form :

(x-h)² = 4a(y-k)   ;

Now we have to shift the origin to a new point (h,k) from the (0,0) point. Also, we have :

X = x – h and Y = y – k  ;          …..(here we have h = 3/2  and k = -11/8)

to find the old points (x,y)  , we simple put the values below as  :

x  =  X + h  and   y  =  Y + k      ;             …….  note this as equation 1

We’ll get the below transformed standard equation of the parabola as given below  :

X² = -2Y     ,     

On comparing the above standard equation with the standard form  X² = -4aY

we have ,  4a = 2  ,   thus    a = 1/2    ;

Now the vertex of this standard parabola is at (X = 0, Y = 0)  , thus the vertex of the given parabola with respect to the new axis are  (0,0)

So now since we’ve shifted the new origin to (h,k) i.e. (3/2,-11/8)  . Thus the vertex of the parabola with respect to the old axes are (3/2,-11/8)         ………….(by putting values of X and Y in equation 1)

The equation of the parabola with respect to the new axes is X = 0 , so the equ of the axis with respect to old axes is x = 3/2  ;                     ……..(by putting the value of  X in equation 1)

The coordinates of the focus with respect to the new axes are (X = 0 , Y = -a) i.e.   (X = 0 , Y = -1/2)  . So the coordinates  of the focus with respect to old axes will be (3/2 , -15/8)      …….  (by putting values of X and Y in equation 1)

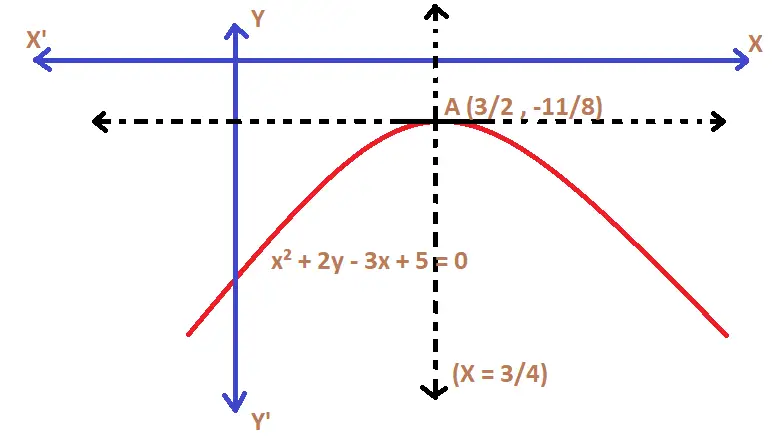
Directrix equation with respect to new axes is Y = a i.e.  Y = 1/2

The equation of the directrix with respect to the new axis will be  ‘y’ = Y – 11/8 =  1/2 – 11/8 =  -7/8     ;

Length of latus rectum is a constant i.e. ‘4a’  , since here a = 1/2  , Thus length = 4a = 4*  1/2 =  2 

How To Find The Vertex Of A Parabola Function In The Form Of A Quadratic Equation ?

A quadratic equation is a second-degree polynomial, having roots (real or complex) on the x-axis of the cartesian plane . Now if we are given a simple quadratic equation of the form below :

f(x) =  ax² + bx + c 

Or f(x)  =  -ax² + bx + c      

For both the given equations above , we will get a parabola shaped graph with minima/maxima on the vertex of the parabola .

Depending upon the sign of the coefficient of ‘a‘ , the parabola will be either have opening upwards (if ‘a’ is positive and here vertex will be the minimum point) or downwards (if ‘a’ is negative and here vertex will be the maximum point)

In simple terms , we can say that the vertex of the parabola is the point at which the graph changes its direction and form a U shaped plot on the graph . There is also an axis of symmetry present on the graph , and vertex will always lie on this axis of symmetry .

Clearly from the above graph , it is much evident that if we find the points where the graph cuts the x-axis (or roots of quadratic equ) , and then if we find the midway between these roots . Then surely we’ll get the x coordinate of the vertex of the parabola (and the axis of symmetry) .

Thus on putting the x value in the given f(x) (quadratic equation)  , we can quickly find the y coordinate of the vertex too .Let’s summarize the steps to find the vertex of the parabola in a quadratic equation:

• Given a quadratic equation
• Find the roots of the quadratic equation
• Find the midpoint of the roots in the x-axis
• Now once the x value is obtained , put this x value in the equation to get the corresponding y value of the vertex

Now the question is , how to find the roots of any quadratic equation (as this is the first step above)

We can find the roots and hence the vertex of the parabola using any of the below-given methods :

• Middle term split up (factorization)
• Quadratic Formula
• Completing Squares

Remember that the aim is to find the roots of any quadratic equation (x intercepts) , then the average value of these when we put this in the equation , we can find the vertex of parabola (i.e. y & x values both) .

With the knowledge of vertex of a quadratic equation , we can further comment on the range and domain values of any parabola as shown below :

f(x) =  x² +  5x  +  6   

Now first we need to plot the graph (also find its roots for the vertex for sure) ,  for this let’s find out the roots :

by using the middle term split up method (factorization) ,  we can write the above function as follows :

f(x)  =  x² +  5x  +  6     =   (x+2)(x+3) =  0  ;

The roots of the above equation is the point where f(x)  =  0  ;

Hence the roots will be given as x  =  -2 , -3 ;

Now plotting the graph for the same :   

f(x)  =  x² +  5x  +  6   ;   the graph will look like as follows :

 

Clearly the domain is R  i.e.  (-∞,∞)          …..(since there is no endpoint along the x-axis if we go from left to right) 

Now range will be given as the points along the y-axis : 

As seen in the graph , there is no endpoint of the graph in the upward direction along the y-axis. Now the start point of the graph is given as ‘vertex‘ 

where , the axis of symmetry   =   midpoint of both the roots on the number line (vertex always lies in this line)

Also ,  for the y-coordinate of the Vertex of f(x)   =    Put the value of ‘x‘ if equ of f(x)       …… (x is the axis of symmetry)

hence x value of vertex = (-2-3)/2  =  -2.5

On putting this value on f(x)  , we get the y value as = (-2.5)² – 5*2.5 + 6 = -1/4 =  -0.25  

Vertex of the given parabola  =  (-2.5 , -0.25)

Now the graph will cut the y-axis at some point where ,    x = 0  

f(x)  =  x² +  5x  +  6 ;

On putting x =0  ,  f(x)  = 6  ;

Now from the graph it is clear that the range of f(x) is given as  [y coordinate of vertex,∞)

Shortcut tip :  the vertex for any quadratic function can be given as the formula :

Vertex =   (-b/2a ,  -D/4a)   ,  where  D  =  b² – 4ac         for the equation  f(x)  =   ax²  +   bx    +  c    ;  

On applying the formula , in the equation :  f(x)  =  x² +  5x  +  6   ;  

a = 1  ,  b  =  5  and c = 6    ,  Also D =  1  

Vertex of  f(x)  =   (-5/2 ,  -1/4)   

The range of f(x)  is [-1/4 ,  ∞)   

We can also solve this using the quadratic formula as :

x1 = [-b + √(b² – 4ac)] /2a       and      x2   =  [-b – √(b² – 4ac)] /2a    ;

a = 1  , b = 5   and c = 6

With the above values , we will get the two points on the x axis as same i.e. -2 and -3 . 

Note : If you are lucky enough, then only you’ll get the nice looking (easy) roots as above . Elsewhen you can’t able to do factorization,then try to solve it using this quadratic formula method to find the complex two roots.

The same is the case for the completing squares method for any quadratic equation. Let’s look into that in the next section and try to derive the vertex form of parabola in detail .

How To Find The Vertex Of A Parabola In Vertex Form (Using Completing Squares) ?

Now we will find the vertex of parabola using the completing squares method . So let us look into one simple quadratic equation again to make this concept clear :

f(x)  =  2x² – 8x + 1   ;

Now the above equation can be written as ,

f(x)  =  2(x²  –  4x)   +  1

or  f(x)   =  2(x²  –  4x  +  4  –  4)   +  1

now we’ll use the completing squares method , where we gonna add and subtract ‘4’  to make use of the identities i.e. either (a+b)² or (a-b)²

The terms we need to add & subtract depends upon the term already present in the RHS i.e. ‘x²  –  4x’  here . The sole motto of this is to reduce the RHS into an identity i.e. either (a+b)² or (a-b)²

Tip : To find the term needs to be added and subtracted to make a square term in the RHS , just simply add & subtract the term i.e. (half the coefficient of ‘x’ in the RHS )²  ,  in this case we have ‘4x’  

f(x)  =  2[(x – 2)² – 4]   +  1      ;

f(x)   =   2(x – 2)²  –  8  +  1   ;  

i.e.   f(x)   =  2(x – 2)²  –  7

The above resultant equation  is the standard equation of the  vertex form of the parabola , this is given as follows :

  y =  a(x – h)² + k 

here the point of vertex is given as (h,k) . Also there are three constant values in the above vertex form i.e. h , k and a 

x and y are variables in the above equation . Thus now in the below equation i.e. 

f(x)   =  2(x – 2)²  –  7       ;

The vertex of the parabola is at (h,k)  i.e. (2,-7)  . Clearly from the vertex of parabola , we can predict two important things i.e. the axis of symmetry and the minimum/maximum value quickly . 

For the above quadratic equation , f(x)  =  2x² – 8x + 1 ,  it will open upwards (positive coefficient of x²) , thus here the vertex will give the minimum value of the equation .

Also, the x value of the vertex will be the Axis of Symmetry. As we already know that the vertex of parabola lies on the axis of symmetry  i.e. x = 2

How To Find Equation Of Parabola With Two Points Given (Including Vertex) ?

Given the vertex and one another point given explicitly , we can easily derive the equation of parabola using the vertex form of parabola as seen above i.e. 

y =  a(x – h)² + k 

Now here we know that (h,k) is the coordinates of the vertex of parabola . Thus if we are given the vertex of parabola as (2,-7) and one point that lies on the parabola is (0,1) . Now we want to find the complete equation of parabola from these two points.

Putting the values in the vertex form of a parabola as below :

y =  a(x – h)² + k                     ;

Now put the point of vertex above (2,-7) in place of (h,k)    

y =  a(x – 2)² –  7    ;

Now put the point (0,1)   in the above equation to find the value of constant ‘a’ 

i.e.       1  =  a(0 – 2)²  –  7

Then ,         1  =   4a  –  7    which will give  value of    ‘a’  =  8/2  =  4  ;

Now the final equation of parabola will be :

y =  a(x – 2)² –  7    ;

Hence ,   y =  2(x – 2)² –  7    ;

On simplifying ,   f(x)  =  y  =   2x² – 8x + 1   ;

Hope you really liked this post regarding the various methods to find the vertex of parabola and also in quadratic equation correctly . Let me now if you have any doubts in the comments section .