How To Find Arc Length And Area Of Sector In Circle ? (With Examples)

There are many geometric shapes we encounter in mathematics precisely. Some of the most common plane figures such as rectangles, squares, triangles, etc can be used to find the area and perimeter of any Complex figure. In this post, we will mainly focus on the circular shape and the various parts of the circle to find the area of sector and length of an Arc.

We indeed encounter circular shapes like the cycle wheels , wheel Arrow, bangles, and other circular parts in our daily life. Firstly we will start with the basics of the circle and then we’ll move further to find the arc length and the area of sector.  (OP and OQ are radius below with center ‘O’)

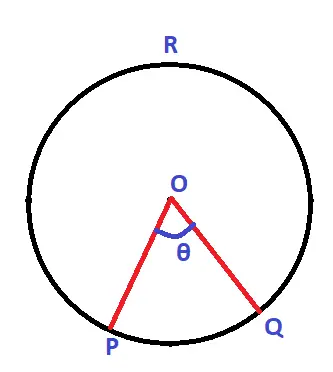
In mathematics, we can define a circle as a plane figure having the locus of a point that moves in such a way that its distance from a fixed point always remains the same. The fixed point is the center of the circle and the distance from the center is the radius.

How To Find Arc Length In A Circle ?

Steps to be followed to find the Arc length of a circle (formula) :

• Firstly, try to find the radius of the circle . 
• Now once we get the radius , try to find the sector of the circle for which the given arc is the boundary 
• Then find the angle subtended by this arc at the center of the circle 
• Finally apply the below formula  to find the arc length :  

                                                Arc Length Formula :  (θ/360)  ×  2πr 

Where ‘2πr’ is nothing but the circumference of the circle with radius ‘r’ .

How To Find Area Of A Sector In A Circle ?

Steps to be followed to find the Area of A Sector in a circle (formula) :

• Firstly, try to find the radius of the circle. 
• Now once we get the radius, try to find the sector of the circle for which the given arc is the boundary 
• Then find the angle subtended by this arc at the center of the circle 
• Finally, apply the below formula  to find the area of the sector of the circle :  

                                                Area of Sector Formula :  (θ/360)  ×  πr² 

Where ‘πr²‘ is nothing but the area of the circle with radius ‘r‘ .

For a complete explanation of the above formulas, just sit back and proceed further to the next sections.

How To Find The Arc Length Of A Circle ?

An arc of a circle is nothing but the portion of the circle’s circumference. That means you may consider an arc as the boundary section of any given circle . Based upon the angle that an arc subtends at the center , it can further be classified as Minor and Major arc of a circle .

The deep red colored part showing the minor arc above as arc PQ

If an angle subtended by the arc is less than 180° at the center, then it is called the minor arc , whereas if the ‘θ‘ value is more than 180° , then it will be the major arc of the circle .

The perimeter of a circle is known as its circumference. For calculating circumference, we can use the formula of circumference as 2πr .

Arc length of a semicircle will be :    (Circumference)/2   =    (2πr)/2    =  πr

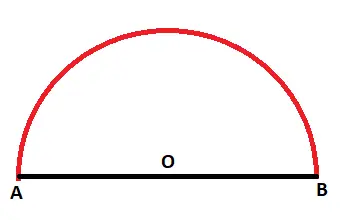
Also by using the formula, we know that the arc of a semicircle will subtend an angle 180° ,  .

Then :                    Arc Length Formula :  (θ/360)  ×  2πr  =    (180/360)  ×  2πr  =    πr

Also ,                    Arc Length Formula :  (θ/360)  ×  2πr    =  (θ/360)  ×  Circumference

Near ‘π‘ the Greek letter having a value equivalent to 3.1416 or in fraction terms it can be denoted as 22/7.
Now the area of the circle is πr² . Area of a semicircle is πr²/2

What Is Sector Of A Circle ?

Now let us understand the meaning of the sector in any circle (the shaded part below). Consider a circle with Centre ‘O’ and radius ‘r’ (OP / OQ). Let’s say we have three points on the circle i.e. the points P , Q and R  respectively on the circumference .

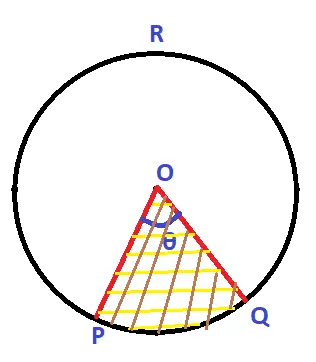
Now if we join the center to two points that are with points P and Q , then we can see that the circle will be divided into two regions namely OPQ and OPRQ .

Each of these two regions is called the sector of the same circle. So now we have a minor sector that is the part OPQ with arc PQ as a part of its boundary. On the other hand, we have the major sector are you with an Arc PRQ as a part of its boundary.

Now the sector of a circle is called a minor sector if the minor arc of the circle is a part of its boundary.

Likewise, a sector of a circle is called a major sector if the major arc of the circle is a part of its boundary.

Now let’s say in the given circle we have a minor sector with an angle ‘θ’ substandard at the center of the circle. Here the major sector has no angle, but we can easily find the angle of the major sector by removing angle theta from 360 degrees (i.e. major sector angle = 360° – θ).

If we add the angle subtended by the major and minor arc of any given circle then the final result will always be 360°.
Similarly, the sum of minor and major arc of any circle is equal to the circumference of the circle.

The sum of the areas of major and minor sectors of a circle is equal to the area of the circle.

In simple words, we can say that a sector mainly consists of a plane figure consisting of two straight lines (radius) with the same starting point (center of the circle), and a curve shape that is the Arc of the circle.

What Is The Area Of Sector In Circle ?

Consider a circle of radius ‘r‘ having its center at ‘O’. Let You Be A sector of the circle such that angle AOB is equal to ‘θ’. If θ is less than 180 degrees , then clearly the arc ABC is a minor arc of the circle.

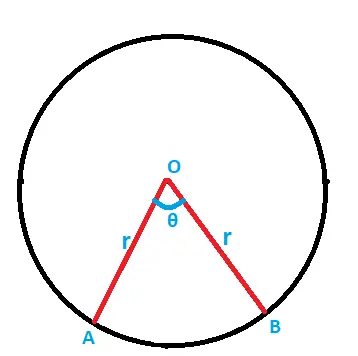
Now if we increase the θ value, then the length of the arc AB also increases and if it becomes 180 degrees then the arc AB becomes the circumference of a semicircle. Hence if an Arc subtends an angle 180° at the center then it’s Arc length is πr .

If the arc subtends an angle of ‘θ’ at the center of the circle, then its Arc length is given by the formula i.e.

Arc Length  :   (θ/180°)  ×  πr

The arc length L of a sector of angle θ in a circle of radius ‘r’ is given by

L  =  (θ/180°)  ×  πr   =   (θ/360°)  ×  2πr  =  (θ/360°)  ×  2πr  =  (θ/360°)  ×  Circumference Of Circle

Hence we can say that:     Arc Length  =  (θ/360°)  ×  Circumference Of Circle

As mentioned above, if the arc subtends an angle 180° ,  then the area of a corresponding sector is equal to the area of the semi-circle  is given by    πr²/2

Area of Sector Formula :  (θ/360)  ×  πr²  

Relationship Between Area Of Sector And Arc Length In A Circle (Shortcut) ?

As mentioned above, the formula for both can be correlated and can be used to find the other value if any one of these terms is given. Let say if Area of the sector is ‘A’ and Arc length is ‘L’ of a circle with radius ‘r‘ and center ‘O’ , then :

Area of Sector Formula :  (θ/360)  ×  πr²        ;   

Also, we can write that,      A   =    (θ/360)  ×  πr²   =    1/2  ×   [(θ/180)  ×  πr ] ×  r

But then we also know that   Arc length =  L  =  (θ/180)  ×  πr

Finally,  the relationship between  both L and A will be :

A  =  1/2  ×   L ×  r  

Let’s now solve some examples now related to  Sector and Arc length formula in any circle :

If a sector is cut from a circle of radius 21 cm , and the angle of the sector is 150° . Then find the length of arc and area of sector in this circle .

Now here, the radius is given as 21 cm and the angle of the sector is 150°. we already know the formula for the Area of the sector and the arc length.

Area of Sector Formula :  (θ/360)  ×  πr²   

Then ,                     Area  =  (150/360)  ×  πr²    =   (5/12)  ×  (22/7)  ×  (21)²    =   1155/2   =  577.5 cm²

Also ,                      Arc Length Formula =  (θ/360)  ×  2πr    =  (150/360)  ×  2 ×  (22/7) × 21  =  55 cm

This problem is pretty straight forward (isn’t it !) . Now let us see some other type of problems :

The perimeter of a sector is 16.4 cm . Let the radius be 5.2 cm . Now let’s try to find the area of this sector .

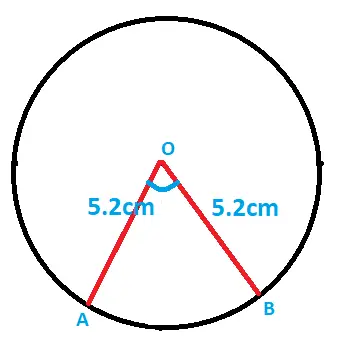
Here the perimeter of the sector is given so ,

OA + OB +  arc  AB  =  16.4 cm  

i.e.    5.2  +  5.2  +   arc AB  =  16.4    ;

Then ,         arc AB =  16.4 –  10.4   =  6 cm  ;

Now let’s try the shortcut formula as mentioned above .

A  =  1/2  ×   L ×  r    ;      here A =  area of sector    and  L  = arc length   

So putting the values of A and ‘r’ , we have :

A  =  1/2  ×   6 ×  5.2   =   15.6 cm²

As evident from the above calculations, the area of the sector is 15.6 cm²  and arc length AB is  6 cm for this given circle.

Hope you really liked this post regarding the various methods to find the Area of sector and arc length of any circle quickly with examples.

Stay tuned for more interesting stuff in this series. Let me know if you have any doubts about this topic .