How To Find Domain And Range Of A Parabola ? (Quadratic Equation With Graphs)

Domain and range of a parabola shaped graph is the first step towards finding the minimum and maximum values of any parabolic function .  If you are still unaware of the basics of domain and range , you can check my previous detailed posts for sure. In this post , we’ll mainly focus on finding the domain and range of a parabola (quadratic equations) . So just sit back and read further .

How To Find Domain And Range Of A Parabola ?

Let’s understand the steps to find the domain and range of a parabola :

• Plot the graph of f(x) i.e. y = f(x) , for this you need to have the knowledge of graphs of basic maths functions
• In any graph, we can have Domain as all the x – coordinate values (along x-axis) of the graph
• And Range is all y – coordinate values (along y-axis) of the graph
• Finally you have to include/exclude the endpoints in the interval carefully by looking at the graph (for which f(x) is a valid function).

The above steps are the same for finding the domain and range of any function graphically . Moreover, there is also a readymade formula to find the minima and maxima of a quadratic function (parabola) . 

You can even find the domain and range of a parabola algebraically , but for everything a basic understanding of parabolic function is necessary . 

What exactly is a Parabola Function ?

The parabolic function is simply a specific type in the family of curves aong others like the ellipse , hyperbola , etc . For any parabolic function  , we’ll see a common shape as the ‘U‘ shaped pattern . 

The parabolic functions are related to the quadratic equations normally . You may also encounter a sideways parabola sometimes . In this post we’ll see the method to find domain and range of any parabola just by inspection quickly . 

Always remember that the degree of a parabolic function will be always ‘2’.

Types Of Parabola And Its Graph !!

There are normally four types of parabola , i.e. a vertical and horizontal parabola indeed . In a vertical parabola , we’ll have either an Up or Down facing parabola like below :

In a vertical parabola  , the upwards or a downwards opening is basically based upon the sign of the coefficient of x² in the quadratic equation .  

In the equation f(x) =  ax² + bx +c 

for   a > 0 value :

    

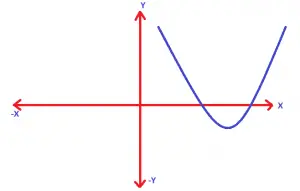
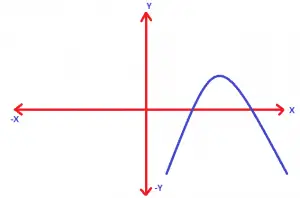
for   a < 0 value :

Now for horizontal parabola , we basically have a function defined in terms of ‘y’ variable i.e. :

f(y)  =  ay²  +  by  + c  

Again depending upon the sign of ‘a’ , the graph opening will be different :

for   a > 0 value :  

 

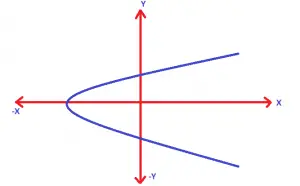
for   a < 0 value :    

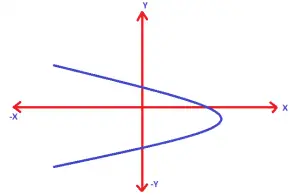
Now , hopefully the types of parabola is pretty clear to you . Lets now understand the process to solve fprdomain and range in parabolic function . 

Now clearly, the minimum and maximum value of any parabola will depend upon the shape of the graph firstly . For example in an upward-opening vertical parabola, we’ll have the minimum point at the vertex of the parabola and the maximum value of the function should be always infinity as shown :

Domain And Range Of A Square Function Using Graph  !!

A parabola is formed whenever we have two values of ‘x’ , that will give same value for the f(x) . Basically we are talking about the square function here . 

A parabolic function will always resemble a symmetric nature along the axis of symmetry . This U shaped graph is thus due to the possible same value of ‘f(x)’ for two ‘x’ values . 

First, let us understand the concept of a square function along with its graph. 

A square function will always result in a positive value , but it can accept any values in R . The square function is given by :

         f(x)   =   x²   ,      is a square function .

Let’s plot the graph of f(x) as given below   :

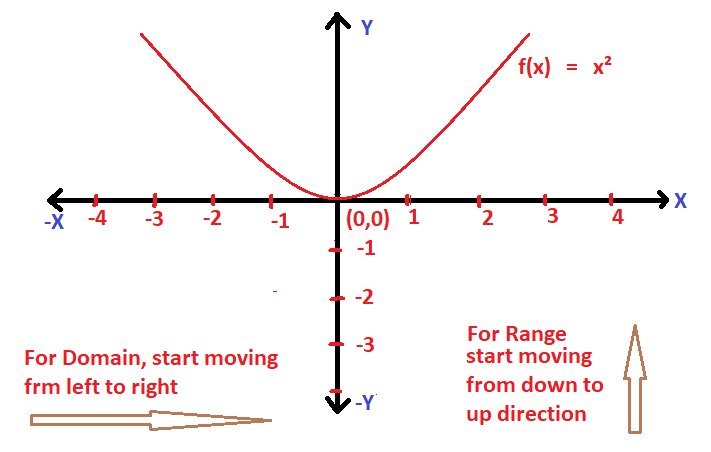
Clearly the domain of f(x) is R  i.e.   (-∞ , ∞)   and the range of f(x)   is  [0,∞) ,  the graph of a square function is a parabola .  

Now let’s try to find the domain and range of functions other than the standard function graphically . Always just keep in mind that in order to find the domain and range of a graph , you have to follow the below steps :

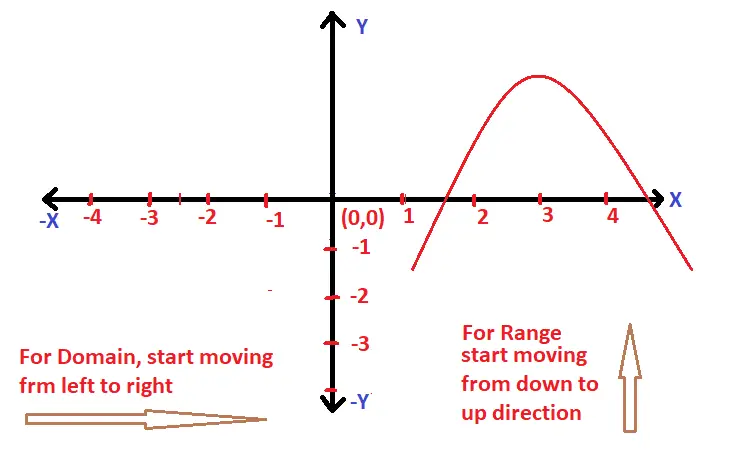
1. For finding domain graphically, just start to move in the direction from the Left to Right along the x-axis .

2. Now for finding the range of a graph , just move from Down to Up direction along the y-axis , 

The above two points will be clear from solving some examples to find domain and range graphically . 

How To Find Domain And Range Of A Parabola (Quadratic Function)  ?

Now this is interesting. Firstly you have to plot the graph of the given quadratic function i.e. a parabola shaped plot precisely . Also, the opening of the parabola will depend on the coefficient of x² in the quadratic equation . 

Let say      f(x)  =   ax²  +   bx    +  c   

Now the above equation is the standard quadratic equation ,  we can have different shaped parabola lying anywhere in the cartesian plane depending upon the roots and sign of the coefficient of ‘x²’ 

If a > 0   , then the graph of f(x) will be : 

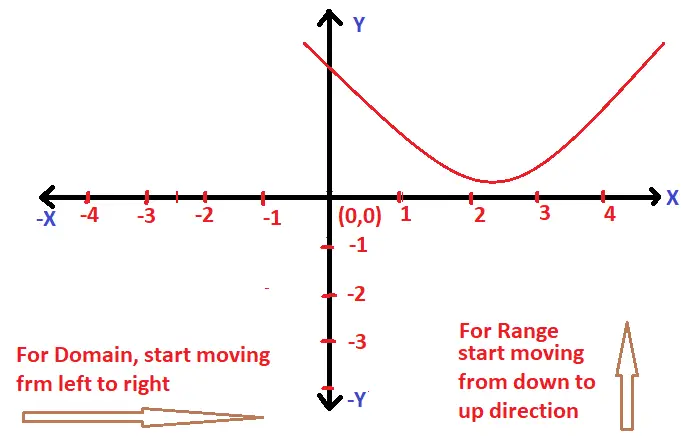
If a < 0   , then the graph of f(x) will be : 

Also remember that the domain of any vertical parabolic equation will always be R  i.e.  (-∞,∞)  , which means that it can take any value for ‘x’ , and for the range we need to care for the start and endpoint of the quadratic equation along the y-axis .  Let’s try an example now to make this concept clear :

Now let us try to find the domain and range of the below parabolic function graphically :

f(x) =  x² +  5x  +  6   

Now first we need to plot the graph ,  for this let’s find out the roots :

by using the middle term split up method ,  we can write the above function as follows :

f(x)  =  x² +  5x  +  6     =   (x+2)(x+3) =  0  ;

The roots of the above equ is the point where f(x)  =  0  ;

Hence the roots will be given as x  =  -2 , -3 ;

Now plotting the graph for the same :   

f(x)  =  x² +  5x  +  6   ;   the graph will look like as follows :

 

Clearly the domain is R  i.e.  (-∞,∞)          …..(since there is no endpoint along the x-axis if we go from left to right) 

Now range will be given as the points along the y-axis : 

As seen in the graph , there is no endpoint of the graph in the upward direction along the y-axis. Now the start point of the graph is given as ‘vertex‘ 

where , the axis of symmetry   =   midpoint of both the roots on the number line

Also ,  for the y-coordinate of the Vertex of f(x)   =    Put the value of ‘x‘ if equ of f(x)       …… (x is the axis of symmetry)

Now the graph will cut the y-axis at some point where ,    x = 0  

f(x)  =  x² +  5x  +  6 ;

On putting x =0  ,  f(x)  = 6  ;

Now from the graph it is clear that the range of f(x) is given as  [y coordinate of vertex,∞)

Shortcut tip :  the vertex for any quadratic function can be given as the formula :

Vertex =   (-b/2a ,  -D/4a)   ,  where  D  =  b² – 4ac         for the equation  f(x)  =   ax²  +   bx    +  c    ;  

On applying the formula , in the equation :  f(x)  =  x² +  5x  +  6   ;  

a = 1  ,  b  =  5  and c = 6    ,  Also D =  1  

Vertex of  f(x)  =   (-5/2 ,  -1/4)   

The range of f(x)  is [-1/4 ,  ∞)   

For the above parabolic function , since it is vertical (upward-opening) parabola and hence a thumb rule will be that the domain of a vertical parabola will always be same i.e. (-∞ , ∞) in the number line . 

Similarly, for a horizontal parabola the range will be R , as the endpoint will be ∞ in both the direction along the y – axis . 

Hope you really enjoyed this post regarding the basics of parabola . Stay tuned for more interesting stuff in this series .