Equation Of A Circle In It’s Standard Form And Some Examples With Steps !!

July 8, 2020 Techie Aric 0 Comments

‌

A circular shape is indeed one of the basic geometric figures we encounter in our daily life. In this post, we will explore the in-depth details and also the standard equation of a circle. Further, we’ll see some of the common examples related to the equation of circles. So firstly we need to understand what exactly a circle equation resembles. In any circle, we precisely require a center and radius as its only parameters to define it completely.
‌

What Is The General Equation Of A Circle ?

Let’s first understand the general equation of a circle in brief. So the standard equation of a circle with center (h,k) and radius ‘a’ is given as :

Equation of circle : (x – h)² + (y – k)² = a²

Simply , we can have the general equation of a circle is written in the form as x² + y² + 2gx + 2fy + c = 0 ;

In the above equation, we have three arbitrary constants i.e. g , f , and c , whereas there are two variables i.e. x and y

Here in the above general equation, the center of the circle is given as (-g , -f) and the radius of the circle is $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$

The above equation will be clear as you proceed further in this post. You’ll get all the details and also the example problems related to this circle’s equation.

What Is Circle In Exact Mathematical Terms ?

The mathematical definition of a circle is a geometric figure representing the locus of a point which moves in a plane in such a way that its distance from a fixed point in that plane is always a constant value.

Now here the fixed point is called the center of the circle and the constant distance is called the radius of the circle.
‌

Equation Of A Circle

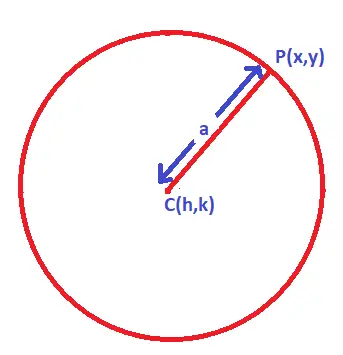
‌An equation of a circle basically means that a generalized equation of the circumference, the equation will give the relation between the coordinates of the moving point P(x,y) involving some constants depending upon the position of the center and the length of the radius.

In simple words, we can say that an equation of a circle nearly represents the set of all points lying on the circumference of the circle.
‌

So the standard equation of a circle with center (h,k) and radius ‘a’ is given as :

Equation of circle: CP² = a² ; ……(applying distance formula i.e. the distance between two points i.e. between C (h,k) and P (x,y) and squaring both sides)

(x – h)² + (y – k)² = a² ;‌

Now let’s see some general cases and the equation of a circle in special cases . So in the next section , we’ll dig deeper to find out the equation of a circle .

How To Find The Equation Of Any Circle Whose Center And Radius Are Given ?

Let ‘O’ be the center of the circle and coordinates be (h,k) . Now let’s assume point P(x,y) be any random point moving on the circumference of the circle. Now from coordinate geometry, we already know that the distance between two coordinates is given by :

Distance OP = $\sqrt { ({ (x-h) }^{ 2 } - { (y-k) }^{ 2 }) }$

Now this distance will be the radius of the circle, let say the radius is a constant ‘a’ . Now applying the distance formula (squaring both side), we will get the following generalized standard equation of a circle :

(x – h)² + (y – k)² = a² ;‌

Now let’s see some special cases of this equation and also derive the equation of the circle in each case :

Equation Of A Circle

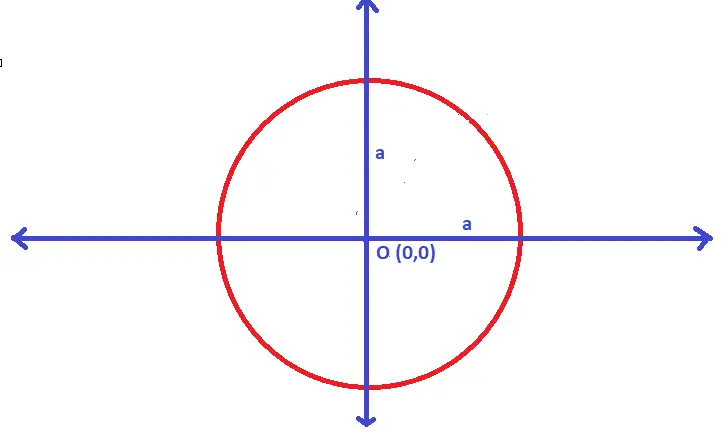
Case 1. Circle equation with center at origin (0,0)

If the center is at origin i.e. O(0,0) . Then putting values of (h,k) as (0,0) in the above standard equation of circle , we’ll get the equation of the circle :

x² + y² = a²

Equation Of A Circle

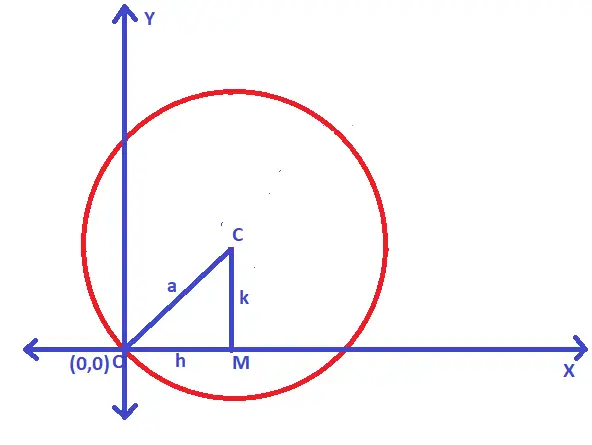
Case 2. When the circle passes through the origin

Let us understand this case using proper diagrams as below :

In the right triangle OCM , we can apply the Pythagoras theorem as below :

OC² = OM² + CM² i.e. a² = h² + k² …………. (1)

We already know the standard equation of the circle as

i.e. (x – h)² + (y – k)² = a² ;‌

Now from equ (1) , putting the value of the term ‘a²’ in the above equation :

(x – h)² + (y – k)² = h² + k² ;

On simplifying the above , the circle equation is given as = x² + y² – 2hx – 2ky = 0

Thus , if the circle passes through the origin (0,0) , then we have the equation of the circle as given above.

Equation Of A Circle

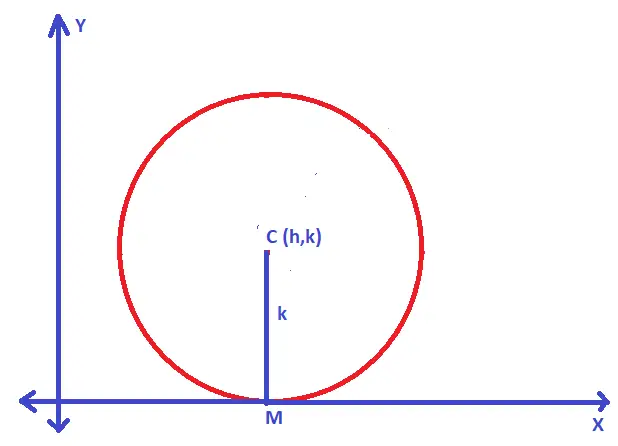
Case 3. When the circle touches the x-axis

Let us understand this case using proper diagrams as below :

If (h,k) is the center of the circle and if the circle touches the x-axis , then :

Clearly, a = k (i.e. the radius of the circle) ……equation (1)

We already know the standard equation of the circle as

i.e. (x – h)² + (y – k)² = a² ;‌

Now from equ (1) , putting the value of the term ‘a²’ in the above equation :

(x – h)² + (y – k)² = k² ;

On simplifying the above , the circle equation is given as = x² + y² – 2hx – 2ay + h² = 0

Thus , if the circle touches the x-axis, then we have the equation of the circle as given above.

Standard Equation Of A Circle

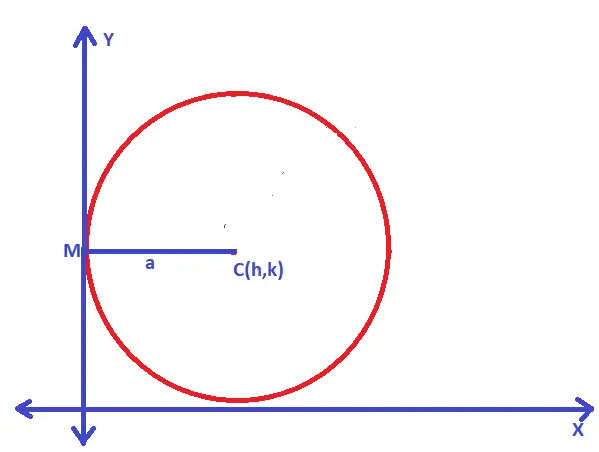
Case 4. When the circle touches the y-axis

Let us understand this case using proper diagrams as below :

If (h,k) is the center of the circle and if the circle touches the y-axis , then :

Clearly, a = h (i.e. the radius of the circle) ……equation (1)

We already know the standard equation of the circle as

i.e. (x – h)² + (y – k)² = a² ;‌

Now from equ (1) , putting the value of the term ‘a²’ in the above equation :

(x – h)² + (y – k)² = h² ;

On simplifying the above , the circle equation is given as = x² + y² – 2ax – 2ky + k² = 0

Thus , if the circle touches the y-axis, then we have the equation of the circle as given above.

Standard Equation Of A Circle

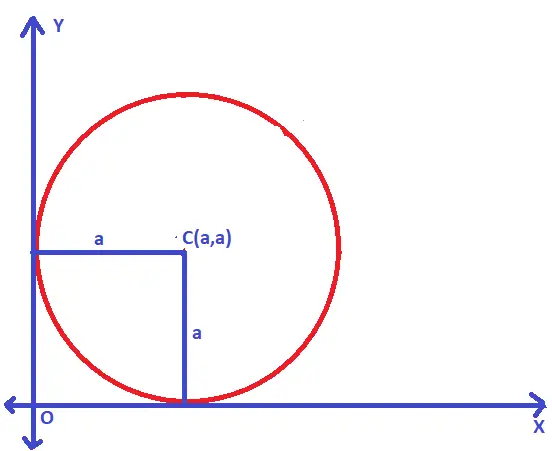
Case 5. When the circle touches both the axes

Let us understand this case using proper diagrams as below :

If (h,k) is the center of the circle and if the circle touches both x-axis and y-axis , then :

Clearly, h = a = k (i.e. the radius of the circle) ……equation (1)

We already know the standard equation of the circle as

i.e. (x – h)² + (y – k)² = a² ;‌

Now from equ (1) , putting the value of the term ‘a²’ in the above equation :

(x – a)² + (y – a)² = a² ;

On simplifying the above , the circle equation is given as = x² + y² – 2ax – 2ay + a² = 0

Thus , if the circle touches both the axes, then we have the equation of the circle as given above.

General Equation Of A Circle

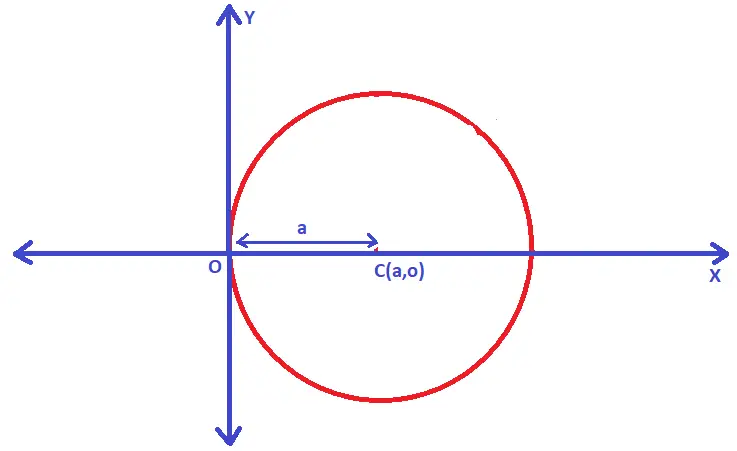
Case 6. When the circle passes through the origin and Center lies on the x-axis

Let us understand this case using proper diagrams as below :

If (h,k) is the center of the circle and if the circle passes through the origin and center lies on x-axis, then :

Clearly, k = 0 and h = a (i.e. as the centre lies on x-axis , y value will be ‘0’) ……..equation (1)

We already know the standard equation of the circle as

i.e. (x – h)² + (y – k)² = a² ;‌

Now from equ (1) , putting the value of the term ‘a²’ in the above equation :

(x – a)² + (y – 0)² = a² ;

On simplifying the above , the circle equation is given as = x² + y² – 2ax = 0

Thus , circle passes through the origin (0,0) and center lies on the x-axis, then we have the equation of the circle as given above.

General Equation Of A Circle

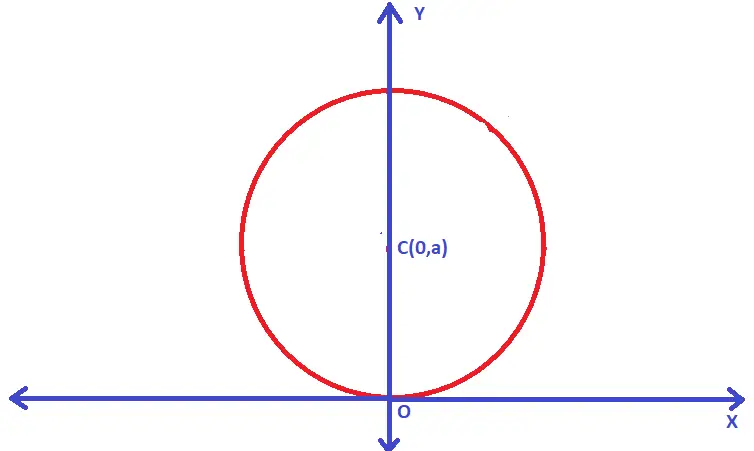
Case 7. When the circle passes through the origin and Center lies on y-axis

Let us understand this case using proper diagrams as below :

If (h,k) is the center of the circle and if the circle passes through the origin and center lies on the y-axis , then :

Clearly, k = a and h = 0 (i.e. as the center lies on y-axis , x value will be ‘0’) ……..equation (1)

We already know the standard equation of the circle as

i.e. (x – h)² + (y – k)² = a² ;‌

Now from equ (1) , putting the value of the term ‘a²’ , h and k in the above equation :

(x – 0)² + (y – a)² = a² ;

On simplifying the above , the circle equation is given as = x² + y² – 2ay = 0

Thus, circle passes through the origin (0,0) and center lies on the y-axis, then we have the equation of the circle as given above.

What Is The General Equation Of A Circle And Its Applications ?

The general equation of a circle as already seen above is given as x² + y² + 2gx + 2fy + c = 0 ;

In the above equation, we have three arbitrary constants i.e. g , f , and c , whereas there are two variables i.e. x and y

Here in the above general equation, the center of the circle is given as (-g , -f) and the radius of the circle is $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$

Now in problems, in order to use this general form of a circle, we need a few easy formulas. Thatis just by looking at any complex second-degree polynomial, you can quickly able to predict the center and radius of the circle.

So if you are given an equation of the below form :

x² + y² + 2gx + 2fy + c = 0 ;

Then simply , center of the circle = (-g , -f) = [-(Coefficient of x)/2 , -(Coefficient of y)/2]

radius of the circle will be = $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$

Now on putting the values for g and f respectively in the above equation for radius :

Radius of circle : $\sqrt { { (\frac { Coefficient\quad of\quad x }{ 2 } ) }^{ 2 }\quad +\quad { (\frac { Coefficient\quad of\quad y }{ 2 } ) }^{ 2 }\quad -\quad Constant\quad term }$

From the radius equation above , we can easily comment about the type of circle i.e.

If $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$ > 0 ⇒ radius of the circle is real and thus the circle is also real

If $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$ < 0 ⇒ radius of the circle is imaginary (centre is real though) and thus the circle is called the imaginary circle

If $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$ = 0 ⇒ radius of the circle is ‘0’ and thus the circle is called as point circle

From the general equation above, some of the observation we can make that can be used to solve the problems quickly are as follows :

general equation : x² + y² + 2gx + 2fy + c = 0 ;

1. The general equation of the circle is quadratic in both x and y variables

2. In the general equation, the coefficient of x² = coefficient of y²

3. If we look carefully, then we can see that there are no terms containing ‘xy’ . We can say that the coefficient of xy is zero always (can be used while solving problems)

4. There are three constant values in the above equation, that is g, f and c.

5. From the radius equation, we can say that there will be 3 standard cases depending upon the sign of the term inside the root as seen above .

Note : For solving problems related to the equation of circles , always keep/make the coefficients of the terms x² and y² as unity i.e. 1

if the coefficient is not 1, then try to make it ‘1’ before solving for different parameters of the circle .

For ex : If the equation of a circle is given as : ax² + ay² + 2gx + 2fy + c = 0 ; and a ≠ 0 then we need to make the coefficients of x² and y² as unity ,

Dividing throughout the equation by ‘a‘ , we can able to get unity coefficient for the above-given circle equation.

x² + y² + 2gx/a + 2fy/a + c/a = 0 ;

The centre is given as : (-g/a , -f/a)

And the radius will be : $\sqrt { { (\frac { g }{ a } ) }^{ 2 }\quad +\quad { (\frac { f }{ a } ) }^{ 2 }\quad -\quad \frac { c }{ a } }$

Steps To Find The Centre And Radius Of A Circle When It’s Equation Is Given !!

Follow the below steps to find the center and radius from any circle equation as given below :

1. We know the general equation of a circle that is

x² + y² + 2gx + 2fy + c = 0 ;

Now in order to find the center and the radius of any circle from the general equation, it is important to make the coefficients of x square and y square as Unity . Then we can apply the formula for the center and the radius of the circle from the equation by putting the constant values.

2. Now apply the formula for the center of the circle from the equation as (-coefficient of x/2 , -coeff of y/2)

3. Now find the radius of the circle from the general equation by using the formula as radius is equal to $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$

Steps For Deriving Equation Of A Circle !!

Now in this section, we’ll try to derive the equation of circle . In order to derive the equation , we can simply prove that the general equation of any circle is given by the equation : x² + y² + 2gx + 2fy + c = 0 ;

So now we can write the above equation as :

x² + y² + 2gx + 2fy + c = 0 ;

Also on adding the terms ‘g² + f²‘ on both the sides of the above equation , we can write :

( x² + 2gx + g² )+ ( y² + 2fy + f² )= g² + f² – c ; ….(taking const term ‘c’ on the right side of equ)

Now , we have : (x + g)² + (y + f)² = g² + f² – c …… equ (1)

As we already know that there is two basic identity in aths as :

(a+b)² = a² + 2ab + b² ;

(a-b)² = a² – 2ab + b² ;

So now , if we take square root on the right side , and squaring the right term at the same time in the equ (1) above :

(x + g)² + (y + f)² = g² + f² – c ……equ (2)

Now we already know that the standard equ of any circle is given as the below form :

(x – h)² + (y – k)² = a² ; …..equ (3)

Comparing the equ (2) with the above standard equation i.e. equ (3) above, also we know that √a * √a = a

then surely we can derive the values as given below :

h = -g and k = -f , also the value of ‘a’ is given as = a = $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$

Now from the standard equ (3) , we already know that the center of the circle is (h,k) and the radius is ‘a’

Thus , from above we can say that the values of the center and radius of the circle in equ (2) as given below :

Center of circle = (h,k) = (-g,-f) …(comparing both the equations)

Radius is given as = a = $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$

hence we have successfully derived and proved that the equation x² + y² + 2gx + 2fy + c = 0 ; is the general equation of circle with center (-g,-f) and radius is $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$

Diameter Form Of A Circle Equation !!

We can also form an equation of a circle if we have two points as the diameter. The equation of the circle drawn on the straight line joining two given points (x1 , y1) and (x2 , y2) as the diameter is

(x – x1)(x – x2) + (y – y1)(y – y2) = 0

Note : If the coordinates of the endpoints of a diameter of a circle are given, then we can also find the equation of the circle by finding the coordinates of the center and the radius.

Example problems of Equation Of A Circle

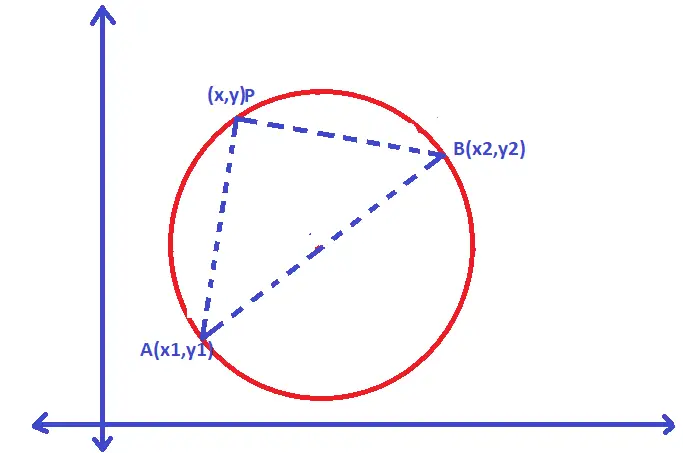
The center is the midpoint of the diameter and radius is half the length of the diameter (where the length can be found out using distance formula)

How To Work Out The Equation Of A Circle ? (Examples Related To Circles Equation Problems !!)

There are many different types of problems related to the equation of circle .

Type 1 : Find the equation of a circle, given its radius and center is given :

If the center of the circle is (2,-3) and the radius is 8, then find the equation of a circle :

We know that the standard equation of a circle with center at (h,k) and radius ‘a’ is

(x – h)² + (y – k)² = a² ;

Now here we are given, center at (2,-3) and the radius is 8

Putting the values in the standard equ above :

(x – 2)² + (y – (-3))² = 8² ;

On solving the above equ : x² + y² – 4x + 6y – 51 = 0

Type 2 : On finding the center and radius of a circle from the given equation of a circle

Let the equation of the circle is given as x² + y² + 6x – 4y + 4 = 0

Now, let’s find the center and radius for the above equation using the standard equation :

(x – h)² + (y – k)² = a²

Here we need to transform the given equation into the standard form as given above. This can be done using the completing squares technique.

Here we need to add and subtract a constant term on both sides of the given equation. The term needs to be added depends upon the coefficient of x or y .

Just remember that you have to add and subtract the term = [(coefficient of x)/2]² + [(coefficient of y)/2]²

Now we have the equation as x² + y² + 6x – 4y + 4 = 0 ;

Try to transform the above equ into the standard form as (x – h)² + (y – k)² = a²

x² + y² + 6x – 4y + 4 = 0 ;

(x² + 6x + 9) + ( y² – 4y + 4 ) = -4 +9 +4 ; …(Adding ’13’ on both the sides)

For the above equ , we can use the identity as (a+b)² and (a-b)² , substituting the values for a and b here and comparing it with the standard equation circle :

(x – (-3))² + (y – 2)² = 3²

Comparing the above with (x – h)² + (y – k)² = a²

We get the center of the circle as (h,k) = (-3,2) And radius of circle is ‘a’ = 3

We can even use the general equation of circle , which is x² + y² + 2gx + 2fy + c = 0 ;

center of the circle is given as (-g , -f) and the radius of the circle is $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$

Now if we are given the equation as x² + y² – 6x + 4y – 12 = 0 ;

The coefficient of x² and y² is unity , so we can simply use the general equation formulas :

center of the circle from the equation as (-coeff of x/2 , -coeff of y/2) = (3 , -2)

Radius of the circle will be = $\sqrt { ({ g }^{ 2 } + { f }^{ 2 } - c) }$

Now on putting the values of g and f from the above general form of equation , we get :

Radius = $\sqrt { { (\frac { Coefficient\quad of\quad x }{ 2 } ) }^{ 2 }\quad +\quad { (\frac { Coefficient\quad of\quad y }{ 2 } ) }^{ 2 }\quad -\quad Constant\quad term }$

That is , radius = √(9+4+12) = 5 ;

Hence the center isat (3,-2) and the radius is 5 units .

Type 3 : Find the equation of circle , given the coordinates of endpoints of the diameter is given

We know that the equation of the circle drawn on the straight line joining two given points (x1 , y1) and (x2 , y2) as the diameter is :

(x – x1)(x – x2) + (y – y1)(y – y2) = 0 …… equ (1)

If the given coordinates are given as (-1,2) and (4,-3) , that is indeed the end points of circle :

Then equation of circle with x1 = -1 , x2 = 4 , y1 = 2 and y2 = -3

Putting the above values in equ (1) , then :

(x – (-1))(x – 4) + (y – 2)(y – (-3)) = 0

On solving the above , the equation of the circle is : x² + y² – 3x + y – 10 = 0

Hope you really liked the above post regarding the equation of a circle with different types of problems and also the steps to derive the circle general equation in detail . Stay tuned for more interesting stuff in this series .

Techie Aric

Aric is a tech enthusiast , who love to write about the tech related products and ‘How To’ blogs . IT Engineer by profession , right now working in the Automation field in a Software product company . The other hobbies includes singing , trekking and writing blogs .

Spread the Wisdom !!