How To Solve Inequality Equations ? (Linear ,Quadratic ,Absolute Values And Fractions/Variable Inequations !!)

July 13, 2020July 13, 2020 Techie Aric 0 Comments

In mathematics, we generally encounter equations in one or two variables. An equation is defined as the statement involving variables and the sign of equality (=) between the RHS (right-hand side) and LHS (left-hand side) of an equation . Similarly, we can define an inequation or inequality as the statement involving variables and with the sign of inequality that is < , > , ≤ or ≥ between RHS and LHS . Following are some of the examples of inequality equations :

3x+ 7 ≤ 0 , 4y ≥ 9 , 6y + 8x < 7 ;

How to solve any Inequality Equations ?

Solving any inequality equations basically means the process of obtaining all possible solutions of the inequality.The solution set of any inequality equation can be found out by following the steps given below:

Step 1 – Obtain the linear/Quadratic/Absolute inequation (derive it, if it’s not given)
Step 2 – Collect all the terms involving the variable on one side (LHS) of the inequality and the constant terms on the other side (RHS) .
Step 3 – Simplify both the sides of inequality in the simplest forms to reduce the inequation in the form i.e ax + b ≤ 0 or ax² + bx + c ≥ 0 etc
Step 4 – Solve the inequality obtained in the above step by dividing both the sides of the inequation by the coefficient of the variable
Step 5 – Write the solution set from the above step in the form of interval notation from the number line
Step 6 – Always remember that the sign of any inequality will never change on adding or subtracting by the same numbers on both the side of the inequality.

However the sign of inequality changes when we divide or multiply with the same negative number on both sides . Also, there is no change of sign on multiplying or dividing by a positive number on both sides respectively.

Types Of Inequality Equations !!

There are several different types of inequality equations you may encounter as given below :

Linear Inequation In One Variable

In this type of inequations, we generally have a single variable and then the equation is of the form as :

ax + b ≥ 0 , ax + b ≤ 0 , ax + b < 0 and ax + b > 0 ;

Linear Inequations In Two Variables :

Let a ,b and c be the non zero real numbers and x , y be the variables. Then this type of inequalities in two variables can be represented :

ax + by ≥ c , ax + by ≤ c , ax + by < c and ax + by > c ;

i.e. 3x + y < 6 , 7y + 5x ≤ 8 etc are some examples of this type .

Quadratic Inequations

Let a, b and c be the non zero real numbers . Then the quadratic inequation is given by

ax² + bx + c ≥ 0 , ax² + bx + c ≤ 0 , ax² + bx + c < 0 and ax² + bx + c > 0 ;

The steps to solve each of the above types of inequalities is different and required a unique approach to solve them precisely .

List Of Inequalities Rules !!

In this section , we’ll mainly discuss the rules you need to follow related to any inequalities equation. Below are the three inequalities rules mentioned as follows :

1. The same number may be added or subtracted from both sides of an equation without changing the sign of inequality.

2. Both sides of an equation can be multiplied or divided by the same number without changing the sign of inequality. However, the sign of inequality is reversed when both sides of an equation are multiplied a divided by a negative number.

3. Any term of an equation may be taken to the other side with the sign changed without affecting the sign of inequality.

Note : Before we dig deep into this topic , it’s important to know (recap) about the brackets used for marking intervals on the number line . Always remember that while finding a solution set of any inequalities, we’ll mainly use two types of brackets :

1. Round brackets (also called parathesis) – To represent the values without including the endpoint (a point on the x-axis in open interval) .

2. Square Brackets – To represent the values including the endpoint (a point on the x-axis in the closed interval)

For eg : if the interval is given by [2,5) ⇔ This means that the values of the x are all the values in the interval between 2 to 5 , also including the value (point) ‘2’ and excluding the point ‘5’ on the number line as shown below :

How To Solve Inequality

Tip : The extreme values in the x-axis i.e. the points ‘infinity‘ and ‘-infinity‘ will never be attached with the square brackets i.e. the infinite point ‘∞‘ should never be associated with the square brackets whatsoever.

Steps to solve linear inequalities In One Variable

In this section, we basically deal with the inequations in one variable as seen above. This is mainly of the below forms :

ax + b > c or ax + b < c or ax + b ≤ c or ax + b ≥ c ;

Let us now solve some examples, following the steps given above to deal with the inequalities.

Let say , we have linear inequations as : 7x + 9 > 30

We have 7x + 9 > 30 ;

Now , 7x > 21

dividing both the sides with ‘7’ , we get :

i.e. 7x/7 > 21/7

Finally , x > 3 , now on plotting this on the number line :

How To Solve Inequality in one variable

The final solution set for this simple inequality example is (3 , ∞)

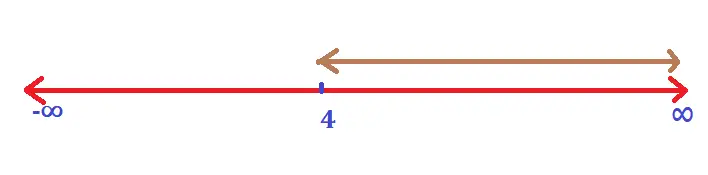
Let’s solve now for the next inequality example : 4x – 16 ≥ 0 ;

On solving, 4x ≥ 16 ;

Dividing ‘4’ into both sides :

i.e. x ≥ 4, plotting this on the number line, we finally get the resultant interval on the number line as [4 , ∞) :

Steps For Solving Inequalities With Variables On Both Sides !!

Now in this section, we’ll look into the one more variety of the linear inequations having variables on both the sides of the equations .

This is basically of the form :

ax + b < cx + d or ax + b > cx + d or ax + b ≥ cx + d or ax + b ≤ cx + d ;

Now let’s solve the given inequation as : 5x – 3 < 3x + 1

Now here, we’ll first shift all the variables on the LHS and will keep the constants on the RHS . Shifting the term ‘3x’ on the left side of the equation , we get :

we have 5x – 3x < 4 ;

Now , 2x < 4 ;

Finally , on dividing by ‘2’ on both sides :

i.e. x < 2 , on plotting this on number line :

Solving Inequalities With Variables On Both Sides

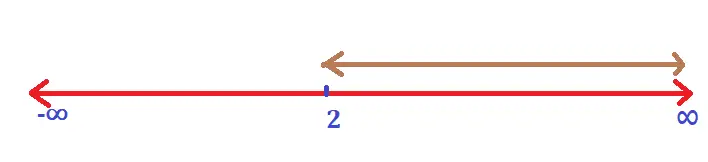
we finally get the resultant interval on the number line as (2 , ∞) as the solution set for the given inequality with variables on both sides .

How To Solve Inequalities With Fractions And Variables In The Denominator ?

Whenever we have any fractions and rational functions/variables in the denominator , then we need to use some additional steps to solve this kind of inequalities .By fractions ,we mainly mean the equations of the form p/q i.e. :

$\frac { ax+b }{ cx+d }$ < k or $\frac { ax+b }{ cx+d }$

> k or $\frac { ax+b }{ cx+d }$ ≤ k or $\frac { ax+b }{ cx+d }$ ≥ k ;

To solve the inequality with fractions and variables in the denominator, follow the below sequence of steps :

1. Firstly obtain the equation (inequality equation)

2. Now shift all the terms on the LHS . And simplify the LHS of the equation to get the resultant form as below

$\frac { ax+b }{ cx+d }$ < 0 or $\frac { ax+b }{ cx+d }$ > 0 or $\frac { ax+b }{ cx+d }$ ≤ 0 or $\frac { ax+b }{ cx+d }$ ≥ ;

3. Make coefficient of ‘x’ positive in numerator and denominator (if it’s not already) .

4. Now find the critical points by equating numerator and denominator to ‘0’ each separately.

5. Now plot the critical points on the number line. Finally the number line will be divided into separate regions based upon the critical points .

6. Now right most region of the expression will be always positive in the number line and all other regions will be alternatively negative and positive , so start marking a positive sign on the right-most region and then mark the positive and negative signs alternatively to other regions

7. Now depending upon the inequality sign, we need to select the appropriate regions from the number line. Now finally write this region in the form of interval notation.

Let’s solve some examples to illustrate the above-given steps further. Let say we want to solve the below inequality :

$\frac { x-2 }{ x+5 }$ > 2 ;

Here we have fractions and variables in the denominator. Just follow the above-listed steps :

from step 2 above, we’ll shift all the terms to the left side i.e.

$\frac { x-2 }{ x+5 }$ – 2 > 0 ;

$\frac { x-2-2(x+5) }{ x+5 }$ > 0 ;

Then , $\frac { x-2-2x-10 }{ x+5 }$ > 0 ;

Now, $\frac { -x-12 }{ x+5 }$ > 0 ;

As per step 3 above , we want a positive coefficient for ‘x’ . Hence multiplying with ‘-1’ both the sides of the above inequality , the sign of inequality will also change as :

Finally the inequality will be : $\frac { x+12 }{ x+5 }$ < 0

Now from step 4 above ,we have to find the critical points respectively .

In the numerator, we have ‘ x + 12 ‘ term. On equating this to ‘0’ , we’ll get the critical point i.e.

x + 12 = 0 ;

Then , x = -12 ;

similarly, in the denominator we have the term as ‘ x + 5 ‘ , On equating this to ‘0’ , we’ll get another critical point i.e.

x + 5 = 0 ;

Then , x = -5 ;

we obtain the critical points as x = -12 , -5 . Now we’ll plot these points on the number line . The real line will be divided into three regions as shown below :

Solve Inequalities With Fractions And Variables In The Denominator

As per step 6 above, we’ll start marking signs (+/-) for each region on the real line. So we’ll start by a positive sign for the rightmost region, then following a negative and positive sign alternately :

Solve Inequalities With Fractions And Variables In The Denominator

Note : the positive and negative signs above indicates the value of the given inequality equation as ‘all positive’ or ‘all negative’ values in that specific interval .

Clearly the solution set for the given inequality i.e. $\frac { x+12 }{ x+5 }$ < 0 ;

is the region having a set of all negative values i.e. the interval (-12,-5)

Note : We can’t include the points as we don’t have any equality sign in between. Also at x = -5 , the given function will become undefined (since denominator will become zero).

How To Solve Quadratic Inequalities ?

In the case of any quadratic equation , we’ll again need to follow the concept of critical points (or roots) as mentioned above . Steps to be followed here as follows :

1. Firstly obtain the quadratic equation (inequality equation)
2. Now shift all the terms on the LHS . And simplify the LHS of the equation to get the resultant form as below

ax² + bx + c ≥ 0 , ax² + bx + c ≤ 0 , ax² + bx + c < 0 and ax² + bx + c > 0 ;

3. Make the coefficient of ‘x²’ positive .

4. Now find the critical points by equating to 0.

5. Now plot the critical points on the number line. Finally, the number line will be divided into separate regions based upon the critical points .

7. Now depending upon the inequality sign, we need to select the appropriate regions from the number line. Now finally write this region in the form of interval notation.

Let’s find out the solution for the given quadratic inequality as below :

x² + 5x – 15 ≤ -21 ;

From step 1 , shifting everything to the left side :

x² + 5x – 15 + 21 ≤ 0 ;

Then we have the quadratic inequality as : x² + 5x + 6 ≤ 0 ;

As per step 3 above , we want a positive coefficient for ‘x²’ . (here it’s already positive , so no worries)

Now as per step 4 , we’ll now find the roots of the given quadratic inequality :

Using factorization method we can write : (x + 2)(x + 3) ≤ 0 ;

Thus , we have two critical points of this quadratic equ as x = -2 , -3 . We now plot these points in the number line .

As per step 6 above, we’ll start marking signs for each region. So we’ll start by a positive sign for the rightmost region , then following a negative and positive sign alternately :

Solve Quadratic Inequalities

Now clearly we have the three separate regions above , out of which the required solution set for the given quadratic inequality is the region in between point -2 and -3 (giving a negative value). So the solution set is given by [-2,-3] .

Note : We included both the points here, as we have an equality sign in between in the above inequality equation.

How To Solve Inequalities With Absolute Values ?

If we have absolute values, then we need to use some standard results to solve the inequations including absolute values as given below.

Let a ,b and r be any positive real numbers, then we have the following results true for any absolute value inequation :

1. |x| < a ⇔ -a < x < a i.e. x ∈ (-a,a)

2. |x| ≤ a ⇔ -a ≤ x ≤ a i.e. x ∈ [-a,a]

3. |x| > a ⇔ x < -a or x > a

4. |x| ≥ a ⇔ x ≤ -a or x ≥ a

5. |x – a| < r ⇔ a – r < x < a + r i.e. x ∈ (a – r , a + r)

6. |x – a| > r ⇔ x < a – r or x > a + r

7. |x – a| ≤ r ⇔ a – r ≤ x ≤ a + r i.e. x ∈ [a – r , a + r]

8. |x – a| ≥ r ⇔ x ≤ a – r or x ≥ a + r

9. a < |x| < b ⇔ x ∈ (-b , -a) ∪ (a,b)

10. a ≤ |x| ≤ b ⇔ x ∈ [-b , -a] ∪ [a,b]

11. a ≤ |x + c| ≤ b ⇔ x ∈ [-b + c , -a + c] ∪ [a + c,b + c]

12. a < |x + c| < b ⇔ x ∈ (-b + c , -a + c) ∪ (a + c,b + c)

The proofs for the above inequalities is beyond the scope of this article (else the length of this post will surely increase :-p)

Now whenever you find any inequalities including absolute values , then simply you need to use the above mentioned results right away . Let’s solve some inequalities examples to make this concept more clear .

Let’s solve the inequality with absolute value given as : |x – 2| ≥ 5

Here we have the absolute values , this can be solved using the result 8 from the above :

i.e. |x – a| ≥ r ⇔ x ≤ a – r or x ≥ a + r ;

now here we have ‘a’ = 2 and r = 5 , putting these values in the above result for solving the absolute value inequality :

we get |x – 2| ≥ 5 ⇔ x ≤ 2 – 5 or x ≥ 2 + 5 ;

Hence , |x – 2| ≥ 5 ⇔ x ∈ (-∞,-3] ∪ [7,∞)

Finally the solution set for the above given inequality is given as , x ∈ (-∞,-3] ∪ [7,∞)

Solve Inequalities With Absolute Values

Now let’s solve the absolute value inequality example given as a mix of more than one inequations :

Let say the given inequalities are |x – 1| ≤ 5 , |x| ≥ 2 ;

The given system of inequations including absolute values is :

|x – 1| ≤ 5 and |x| ≥ 2 ,

Now in the inequality : |x – 1| ≤ 5 ⇔ |x – a| ≤ r

From result 7 above : |x – a| ≤ r ⇔ a – r ≤ x ≤ a + r i.e. x ∈ [a – r , a + r]

here we have a = 1 and r = 5 , putting the values in the above equ :

|x – a| ≤ r ⇔ a – r ≤ x ≤ a + r = 1 – 5 ≤ x ≤ 1 + 5 i.e. x ∈ [-4 , 6]

Solve Inequalities With Absolute Values

Also , the second absolute inequation we have as : |x| ≥ 2 ;

From result 4 above , |x| ≥ a ⇔ x ≤ -a or x ≥ a ;

here we have a = 2 i.e. |x| ≥ a ⇔ x ≤ -a or x ≥ a = x ≤ -2 or x ≥ 2 ;

Finally the solution set of the above absolute inequality as : x ∈ (-∞ , -2] ∪ [2 , ∞)

Solve Inequalities With Absolute Values

Now combining the solution sets from the above two absolute inequations together . Also for the final resultant inequality solution set ,we need to combine both and the common region will be the final solution set as shown below :

Hence the solution set of the given set of given system of inequations is [-4, -2] ∪ [2 , 6]

Now let’s solve one more variety of inequality example as below :

given inequality is : $\frac { 2 }{ |x-4| }$ > 1 for x ≠ 4 ;

Now the given absolute inequality consists of a fraction value including an absolute value also .

So $\frac { 2 }{ |x-4| }$ > 1 , now mutiplying the term ‘|x – 4|’ on both the sides of the equation we get :

i.e. 2 > |x – 4| , this is of the form |x – a| < r ⇔ a – r < x < a + r i.e. x ∈ (a – r , a + r)

Using result 5 above , we have :

|x – a| < r ⇔ a – r < x < a + r i.e. x ∈ (a – r , a + r) , where a = 4 and r = 2

Putting the values of ‘a’and ‘r’ in the above result :

|x – a| < r ⇔ a – r < x < a + r = 4 – 2 < x < 4 + 2 , i.e. x ∈ (2 , 6)

hence the solution set for the above given absolute value inequality example is x ∈ (2 , 4) ∪ (4 , 6) also x ≠ 4 (since the inequation will become undefined at x = 4)

Solve Inequalities With Absolute Values

We can also solve any inequality equations using graphs . In the next post we’ll discuss this topic in detail along with the various ways of graphing inequalities quickly .

Hope you really liked this post about the in-depth understanding of the inequalities and steps to solve the inequations including fractions. variables , absolute values etc . Let me know in the comments section in case of any doubts .

Techie Aric

Aric is a tech enthusiast , who love to write about the tech related products and ‘How To’ blogs . IT Engineer by profession , right now working in the Automation field in a Software product company . The other hobbies includes singing , trekking and writing blogs .

Spread the Wisdom !!